อย่างที่คุณทราบ ปริมาณทางกายภาพใดๆ เป็นของหนึ่งในสองประเภท มันคือสเกลาร์หรือเวกเตอร์ ในบทความนี้ เราจะพิจารณาลักษณะทางจลนศาสตร์ เช่น ความเร็วและความเร่ง และยังแสดงตำแหน่งที่ความเร่งและเวกเตอร์ความเร็วถูกกำกับด้วย
ความเร็วและความเร่งคืออะไร
ปริมาณทั้งสองที่กล่าวถึงในย่อหน้านี้เป็นลักษณะสำคัญของการเคลื่อนไหวใดๆ ไม่ว่าจะเป็นการเคลื่อนไหวร่างกายเป็นเส้นตรงหรือตามทางโค้ง
ความเร็ว คืออัตราที่พิกัดเปลี่ยนแปลงตามเวลา ในทางคณิตศาสตร์ ค่านี้เท่ากับอนุพันธ์ของเวลาของระยะทางที่เดินทาง นั่นคือ:
v¯=dl¯/dt.
ที่นี่เวกเตอร์ l¯ ถูกกำกับจากจุดเริ่มต้นของเส้นทางไปยังจุดสิ้นสุด
ในทางกลับกัน ความเร่งคือความเร็วที่ความเร็วนั้นเปลี่ยนแปลงไปตามกาลเวลา ในรูปของสูตร เขียนได้ดังนี้
a¯=dv¯/dt.
แน่นอน หาอนุพันธ์อันดับสองของdisplacement vector l¯ ทันเวลา เราก็จะได้ค่าความเร่งด้วย
เนื่องจากวัดความเร็วเป็นเมตรต่อวินาที ความเร่งตามนิพจน์ที่เขียนมีหน่วยเป็นเมตรต่อวินาทีกำลังสอง

เวกเตอร์ความเร่งและความเร็วอยู่ที่ไหน
ในทางฟิสิกส์ การเคลื่อนไหวทางกลใดๆ ของร่างกายมักจะมีลักษณะเป็นวิถีที่แน่นอน หลังเป็นเส้นโค้งจินตภาพบางส่วนซึ่งร่างกายเคลื่อนที่ในอวกาศ ตัวอย่างเช่น เส้นตรงหรือวงกลมเป็นตัวอย่างสำคัญของเส้นทางการเคลื่อนที่ทั่วไป
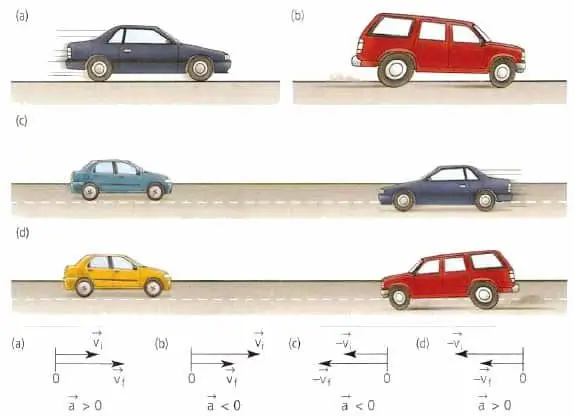
เวกเตอร์ความเร็วของร่างกายมักจะมุ่งไปในทิศทางของการเคลื่อนไหว ไม่ว่าร่างกายจะช้าลงหรือเร่งขึ้น ไม่ว่าจะเคลื่อนที่เป็นเส้นตรงหรือตามแนวโค้ง เมื่อพูดในเชิงเรขาคณิต เวกเตอร์ความเร็วจะพุ่งตรงไปยังจุดโคจรที่ร่างกายตั้งอยู่ในขณะนี้
เวกเตอร์ความเร่งของวัสดุหรือจุดของร่างกายไม่เกี่ยวกับความเร็ว เวกเตอร์นี้มุ่งไปในทิศทางของการเปลี่ยนแปลงความเร็ว ตัวอย่างเช่น สำหรับการเคลื่อนที่เป็นเส้นตรง ค่า a¯ สามารถตรงกับทิศทางด้วย v¯ หรืออยู่ตรงข้ามกับ v¯
แรงที่กระทำต่อร่างกายและความเร่ง
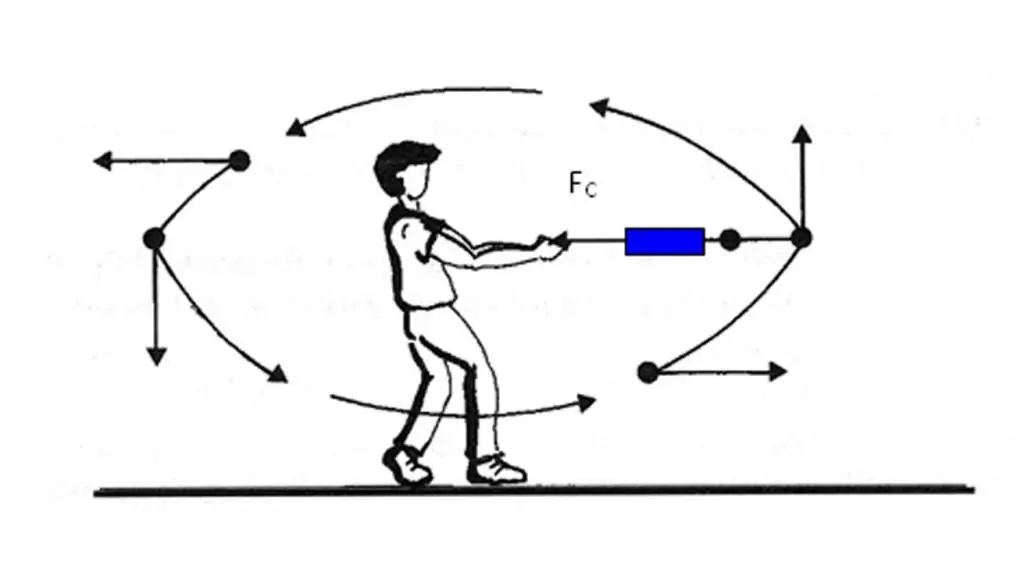
เราพบว่าเวกเตอร์ความเร่งของร่างกายมุ่งสู่การเปลี่ยนแปลงของเวกเตอร์ความเร็ว อย่างไรก็ตาม ไม่ใช่เรื่องง่ายเสมอไปที่จะตัดสินว่าความเร็วเปลี่ยนแปลงไปอย่างไร ณ จุดที่กำหนดในวิถี นอกจากนี้เพื่อกำหนดการเปลี่ยนแปลงความเร็วจำเป็นต้องดำเนินการความแตกต่างของเวกเตอร์ เพื่อหลีกเลี่ยงปัญหาเหล่านี้ในการกำหนดทิศทางของเวกเตอร์ a¯ มีอีกวิธีหนึ่งในการค้นหาอย่างรวดเร็ว
ด้านล่างเป็นกฎหมายที่มีชื่อเสียงและเป็นที่รู้จักของนิวตันสำหรับนักเรียนทุกคน:
F¯=ma¯.
สูตรแสดงว่าสาเหตุของความเร่งในร่างกายคือแรงที่กระทำต่อพวกมัน เนื่องจากมวล m เป็นสเกลาร์ เวกเตอร์แรง F¯ และเวกเตอร์ความเร่ง a¯ จึงอยู่ในทิศทางเดียวกัน ความจริงข้อนี้ควรจำและนำไปใช้ในทางปฏิบัติเมื่อใดก็ตามที่จำเป็นต้องกำหนดทิศทางของปริมาณ a¯
หากแรงที่แตกต่างกันหลายแรงกระทำต่อร่างกาย ทิศทางของเวกเตอร์ความเร่งจะเท่ากับเวกเตอร์ผลลัพธ์ของแรงทั้งหมด
การเคลื่อนที่แบบวงกลมและความเร่ง
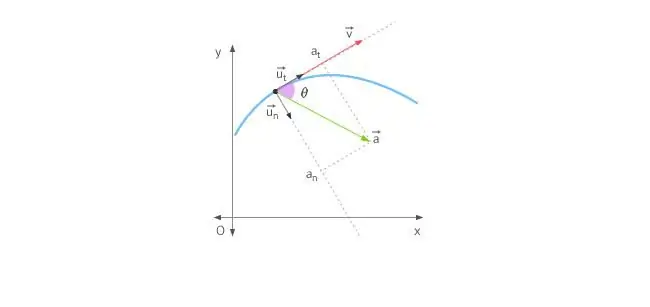
เมื่อร่างกายเคลื่อนที่เป็นเส้นตรง ความเร่งจะพุ่งไปข้างหน้าหรือข้างหลัง ในกรณีของการเคลื่อนที่เป็นวงกลม สถานการณ์จะซับซ้อนเนื่องจากเวกเตอร์ความเร็วเปลี่ยนทิศทางอยู่ตลอดเวลา จากมุมมองข้างต้น ความเร่งทั้งหมดถูกกำหนดโดยองค์ประกอบสองส่วน: ความเร่งในแนวสัมผัสและความเร่งปกติ
ความเร่งในแนวดิ่งมีทิศทางเดียวกับเวกเตอร์ความเร็วหรือตรงข้ามกับมัน กล่าวอีกนัยหนึ่ง องค์ประกอบความเร่งนี้มุ่งตรงไปตามเส้นสัมผัสไปยังวิถี ความเร่งในแนวสัมผัสอธิบายการเปลี่ยนแปลงของโมดูลัสของความเร็วเอง
ความเร่งปกติจะพุ่งไปตามเส้นปกติไปยังจุดที่กำหนดของวิถี โดยคำนึงถึงความโค้งของมันด้วย ในกรณีของการเคลื่อนที่แบบวงกลม เวกเตอร์ขององค์ประกอบนี้บ่งชี้ว่าสู่ศูนย์กลาง กล่าวคือ ความเร่งปกติจะชี้ไปตามรัศมีการหมุน ส่วนประกอบนี้มักเรียกว่าศูนย์กลาง
ความเร่งเต็มที่เป็นผลรวมของส่วนประกอบเหล่านี้ ดังนั้นเวกเตอร์จึงสามารถกำหนดทิศทางของเวกเตอร์ตามเส้นวงกลมได้ตามอำเภอใจ
หากวัตถุหมุนโดยไม่เปลี่ยนความเร็วเชิงเส้น แสดงว่ามีเพียงองค์ประกอบปกติที่ไม่เป็นศูนย์ ดังนั้นเวกเตอร์ความเร่งเต็มจะมุ่งตรงไปยังศูนย์กลางของวงกลม โปรดทราบว่าจุดศูนย์กลางนี้ยังได้รับผลกระทบจากแรงที่ทำให้ร่างกายอยู่ในวิถีโคจร ตัวอย่างเช่น แรงโน้มถ่วงของดวงอาทิตย์ทำให้โลกของเราและดาวเคราะห์ดวงอื่นอยู่ในวงโคจรของมัน

