ปรากฏการณ์และกระบวนการทางธรรมชาติรอบตัวเราค่อนข้างซับซ้อน สำหรับลักษณะทางกายภาพที่แน่นอน ควรใช้อุปกรณ์ทางคณิตศาสตร์ที่ยุ่งยาก และควรพิจารณาปัจจัยสำคัญจำนวนมาก เพื่อหลีกเลี่ยงปัญหานี้ ฟิสิกส์แบบง่ายบางตัวจึงถูกนำมาใช้ ซึ่งอำนวยความสะดวกในการวิเคราะห์ทางคณิตศาสตร์ของกระบวนการอย่างมาก แต่ในทางปฏิบัติจะไม่ส่งผลต่อความถูกต้องของคำอธิบาย หนึ่งในนั้นคือแบบจำลองก๊าซในอุดมคติ พิจารณารายละเอียดเพิ่มเติมในบทความครับ
แนวคิดของก๊าซในอุดมคติ
ก๊าซในอุดมคติคือสถานะของการรวมตัวของสาร ซึ่งประกอบด้วยจุดวัสดุที่ไม่มีปฏิสัมพันธ์ซึ่งกันและกัน ให้เราอธิบายคำจำกัดความนี้ให้ละเอียดยิ่งขึ้น
อันดับแรก เรากำลังพูดถึงจุดที่เป็นวัสดุว่าเป็นวัตถุที่ประกอบเป็นก๊าซในอุดมคติ ซึ่งหมายความว่าโมเลกุลและอะตอมของมันไม่มีขนาด แต่มีมวลที่แน่นอน มันกล้าสามารถประมาณได้โดยคำนึงถึงความจริงที่ว่าในก๊าซจริงทั้งหมดที่ความดันต่ำและอุณหภูมิสูง ระยะห่างระหว่างโมเลกุลจะมากกว่าขนาดเชิงเส้นของพวกมันมาก
อย่างที่สอง โมเลกุลในก๊าซอุดมคติไม่ควรมีปฏิสัมพันธ์ซึ่งกันและกัน ในความเป็นจริง การโต้ตอบดังกล่าวมักมีอยู่เสมอ ดังนั้น แม้แต่อะตอมของก๊าซมีตระกูลก็มีแรงดึงดูดแบบไดโพล-ไดโพล กล่าวอีกนัยหนึ่งมีปฏิสัมพันธ์ของ Van der Waals อย่างไรก็ตาม เมื่อเปรียบเทียบกับพลังงานจลน์ของการหมุนและการเคลื่อนที่เชิงแปลของโมเลกุล ปฏิกิริยาเหล่านี้มีขนาดเล็กมากจนไม่ส่งผลต่อคุณสมบัติของก๊าซ ดังนั้นจึงไม่สามารถนำมาพิจารณาในการแก้ปัญหาเชิงปฏิบัติได้
สิ่งสำคัญคือต้องสังเกตว่าไม่ใช่ก๊าซทั้งหมดที่มีความหนาแน่นต่ำและอุณหภูมิสูงเท่านั้นที่สามารถถือได้ว่าเป็นอุดมคติ นอกจากปฏิกิริยาแวนเดอร์วาลส์แล้ว ยังมีพันธะประเภทอื่นที่แข็งแกร่งกว่า เช่น พันธะไฮโดรเจนระหว่างโมเลกุล H2O ซึ่งนำไปสู่การละเมิดสภาพอุดมคติของก๊าซอย่างร้ายแรง ด้วยเหตุนี้ไอน้ำจึงไม่ใช่ก๊าซในอุดมคติ แต่เป็นอากาศ
แบบจำลองทางกายภาพของก๊าซในอุดมคติ
โมเดลนี้สามารถแสดงได้ดังนี้: สมมติว่าระบบแก๊สประกอบด้วยอนุภาค N สิ่งเหล่านี้อาจเป็นอะตอมและโมเลกุลของสารเคมีและองค์ประกอบต่างๆ จำนวนของอนุภาค N มีขนาดใหญ่ ดังนั้นจึงมักใช้หน่วย "โมล" เพื่ออธิบาย (1 โมลสอดคล้องกับจำนวนของอาโวกาโดร) พวกเขาทั้งหมดเคลื่อนที่ในระดับเสียง V. การเคลื่อนที่ของอนุภาคมีความโกลาหลและเป็นอิสระจากกัน แต่ละคนมีความเร็วที่แน่นอน v และเคลื่อนที่ไปตามทางตรง
ในทางทฤษฎี ความน่าจะเป็นของการชนกันระหว่างอนุภาคนั้นเกือบเป็นศูนย์ เนื่องจากขนาดของอนุภาคนั้นเล็กเมื่อเทียบกับระยะห่างระหว่างอนุภาค อย่างไรก็ตามหากเกิดการชนกันก็จะมีความยืดหยุ่นอย่างแน่นอน ในกรณีหลัง โมเมนตัมทั้งหมดของอนุภาคและพลังงานจลน์ของอนุภาคจะถูกอนุรักษ์ไว้
รูปแบบการพิจารณาของก๊าซในอุดมคติเป็นระบบคลาสสิกที่มีองค์ประกอบจำนวนมาก ดังนั้นความเร็วและพลังงานของอนุภาคในนั้นจึงเป็นไปตามการกระจายทางสถิติของ Maxwell-Boltzmann อนุภาคบางชนิดมีความเร็วต่ำ ในขณะที่อนุภาคอื่นๆ มีความเร็วสูง ในกรณีนี้ มีการจำกัดความเร็วที่แคบ ซึ่งค่าที่น่าจะเป็นไปได้มากที่สุดของปริมาณนี้อยู่ที่ การกระจายความเร็วของโมเลกุลไนโตรเจนแสดงไว้ด้านล่าง
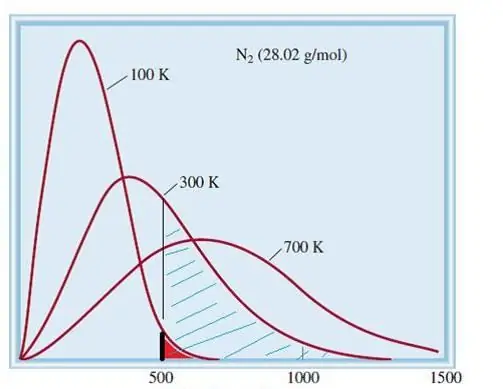
ทฤษฎีจลนศาสตร์ของก๊าซ
แบบจำลองของก๊าซในอุดมคติที่อธิบายไว้ข้างต้นเป็นตัวกำหนดคุณสมบัติของก๊าซอย่างเฉพาะเจาะจง โมเดลนี้ถูกเสนอครั้งแรกโดย Daniel Bernoulli ในปี 1738

ต่อมาได้รับการพัฒนาจนเป็นปัจจุบันโดย August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski และนักวิทยาศาสตร์คนอื่นๆ
ทฤษฎีจลนพลศาสตร์ของสสารของไหล บนพื้นฐานของการสร้างแบบจำลองก๊าซในอุดมคติ อธิบายคุณสมบัติระดับมหภาคที่สำคัญสองประการของระบบตามพฤติกรรมการใช้กล้องจุลทรรศน์:
- ความดันในก๊าซเป็นผลมาจากการชนกันของอนุภาคกับผนังของเรือ
- อุณหภูมิในระบบเป็นผลมาจากการเคลื่อนที่ของโมเลกุลและอะตอมอย่างต่อเนื่อง
มาขยายความสรุปของทฤษฎีจลนศาสตร์ทั้งสองกัน
แรงดันแก๊ส
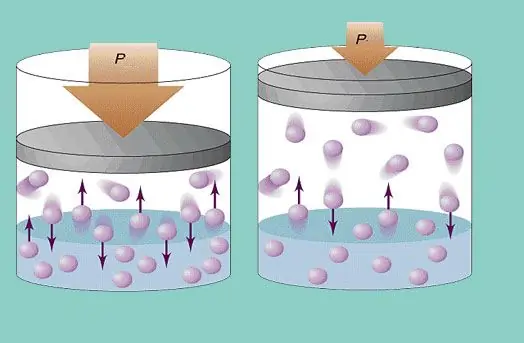
แบบจำลองก๊าซในอุดมคติถือว่ามีการเคลื่อนที่ของอนุภาคในระบบอย่างไม่เป็นระเบียบและการชนกับผนังของเรืออย่างต่อเนื่อง การชนกันแต่ละครั้งถือว่ายืดหยุ่นอย่างยิ่ง มวลอนุภาคมีขนาดเล็ก (≈10-27-10-25 กก.) ดังนั้นจึงไม่สามารถสร้างแรงกดดันในการชนได้มาก อย่างไรก็ตาม จำนวนอนุภาคและจำนวนการชนกันจึงมีมาก (≈1023) นอกจากนี้ ความเร็วกำลังสองรากเฉลี่ยขององค์ประกอบยังหลายร้อยเมตรต่อวินาทีที่อุณหภูมิห้อง ทั้งหมดนี้นำไปสู่การสร้างแรงกดดันต่อผนังของเรือ สามารถคำนวณได้โดยใช้สูตรต่อไปนี้:
P=Nmvcp2 / (3V), โดยที่ vcp คือความเร็วเฉลี่ยของรากที่สอง m คือมวลอนุภาค
อุณหภูมิสัมบูรณ์
ตามแบบจำลองก๊าซในอุดมคติ อุณหภูมิจะถูกกำหนดโดยพลังงานจลน์เฉลี่ยของโมเลกุลหรืออะตอมในระบบที่ศึกษา คุณสามารถเขียนนิพจน์ต่อไปนี้ที่เกี่ยวข้องกับพลังงานจลน์และอุณหภูมิสัมบูรณ์สำหรับก๊าซในอุดมคติได้:
mvcp2 / 2=3 / 2kB ต.
ที่นี่ kB คือค่าคงที่ Boltzmann จากความเท่าเทียมกันนี้ เราจะได้:
T=ม vcp2 / (3kB).
สมการสากลของรัฐ
ถ้าเรารวมนิพจน์ข้างต้นสำหรับความดันสัมบูรณ์ P และอุณหภูมิสัมบูรณ์ T เราสามารถเขียนความเท่าเทียมกันต่อไปนี้:
PV=nRT.
ในที่นี้ n คือปริมาณของสารในโมล R คือค่าคงที่ของแก๊สที่แนะนำโดย D. I. Mendeleev นิพจน์นี้เป็นสมการที่สำคัญที่สุดในทฤษฎีของก๊าซในอุดมคติ เพราะมันรวมพารามิเตอร์ทางอุณหพลศาสตร์สามตัว (V, P, T) ไว้ด้วยกัน และไม่ขึ้นกับลักษณะทางเคมีของระบบแก๊ส

สมการสากลนี้เกิดขึ้นจากการทดลองครั้งแรกโดยนักฟิสิกส์ชาวฝรั่งเศส Emile Clapeyron ในศตวรรษที่ 19 จากนั้นจึงนำสมการนี้ไปใช้ในรูปแบบสมัยใหม่โดย Mendeleev นักเคมีชาวรัสเซีย จึงเป็นที่มาของชื่อนักวิทยาศาสตร์เหล่านี้ในปัจจุบัน

