เอฟเฟกต์แสงทั่วไปที่ทุกคนมักพบเจอในชีวิตประจำวันคือการสะท้อนและการหักเหของแสง ในบทความนี้ เราจะพิจารณากรณีที่เอฟเฟกต์ทั้งสองปรากฏในกระบวนการเดียวกัน เราจะพูดถึงปรากฏการณ์ของการสะท้อนทั้งหมดภายใน
สะท้อนแสง
ก่อนที่จะพิจารณาปรากฏการณ์การสะท้อนแสงภายในทั้งหมด คุณควรทำความคุ้นเคยกับผลกระทบของการสะท้อนและการหักเหปกติ มาเริ่มกันที่อันแรกกันเลย เพื่อความเรียบง่าย เราจะพิจารณาแต่แสงเท่านั้น แม้ว่าปรากฏการณ์เหล่านี้จะเป็นลักษณะเฉพาะของคลื่นในลักษณะใดก็ตาม
การสะท้อนเป็นที่เข้าใจกันว่าเป็นการเปลี่ยนวิถีโคจรเป็นเส้นตรงหนึ่งไปตามลำแสงของแสงที่เคลื่อนที่ไปยังอีกเส้นหนึ่งเป็นเส้นตรง เมื่อกระทบกับสิ่งกีดขวางระหว่างทาง เอฟเฟกต์นี้สามารถสังเกตได้เมื่อชี้ตัวชี้เลเซอร์ไปที่กระจก การปรากฏตัวของภาพท้องฟ้าและต้นไม้เมื่อมองไปที่ผิวน้ำก็เป็นผลมาจากการสะท้อนแสงอาทิตย์เช่นกัน

กฎต่อไปนี้ใช้สำหรับการสะท้อน: มุมอุบัติการณ์และการสะท้อนอยู่ในระนาบเดียวกันพร้อมกับฉากตั้งฉากกับพื้นผิวสะท้อนแสงและมีค่าเท่ากัน
การหักเหของแสง
เอฟเฟกต์การหักเหของแสงคล้ายกับการสะท้อน แต่จะเกิดขึ้นได้ก็ต่อเมื่อสิ่งกีดขวางในเส้นทางของลำแสงเป็นตัวกลางโปร่งใสอีกตัวหนึ่ง ในกรณีนี้ ส่วนหนึ่งของลำแสงเริ่มต้นจะสะท้อนจากพื้นผิว และส่วนหนึ่งจะผ่านเข้าไปในตัวกลางที่สอง ส่วนสุดท้ายนี้เรียกว่าลำแสงหักเห และมุมที่ทำกับแนวตั้งฉากกับส่วนต่อประสานเรียกว่ามุมหักเห ลำแสงหักเหอยู่ในระนาบเดียวกันกับลำแสงสะท้อนและตกกระทบ
ตัวอย่างที่ชัดเจนของการหักเหของแสงคือดินสอหักในแก้วน้ำหรือความลึกที่หลอกลวงของทะเลสาบเมื่อคนดูด้านล่าง

ในทางคณิตศาสตร์ ปรากฏการณ์นี้อธิบายโดยใช้กฎของสเนลล์ สูตรที่สอดคล้องกันมีลักษณะดังนี้:
1 บาป (θ1)=n2 บาป (θ 2).
มุมตกกระทบและการหักเหของแสงแสดงเป็น θ1 และ θ2 ตามลำดับ ปริมาณ n1, n2 สะท้อนให้เห็นถึงความเร็วของแสงในแต่ละสื่อ พวกเขาเรียกว่าดัชนีการหักเหของแสงของสื่อ ยิ่ง n มาก แสงจะเดินทางช้าลงในวัสดุที่กำหนด ตัวอย่างเช่น ในน้ำ ความเร็วของแสงจะน้อยกว่าในอากาศ 25% ดังนั้นสำหรับดัชนีการหักเหของแสงคือ 1.33 (สำหรับอากาศคือ 1)
ปรากฏการณ์การสะท้อนภายในทั้งหมด
กฎการหักเหของแสงนำไปสู่หนึ่งผลลัพธ์ที่น่าสนใจเมื่อรังสีแพร่กระจายจากตัวกลางที่มีค่า n มาก ให้เราพิจารณารายละเอียดเพิ่มเติมว่าจะเกิดอะไรขึ้นกับลำแสงในกรณีนี้ มาเขียนสูตรของ Snell:
1 บาป (θ1)=n2 บาป (θ 2).
เราจะถือว่า n1>n2 ในกรณีนี้ เพื่อความเท่าเทียมกันยังคงเป็นจริง θ1 ต้องน้อยกว่า θ2 ข้อสรุปนี้ใช้ได้เสมอ เนื่องจากจะมีการพิจารณาเฉพาะมุมจาก 0o ถึง 90o ซึ่งภายในฟังก์ชันไซน์จะเพิ่มขึ้นอย่างต่อเนื่อง ดังนั้น เมื่อปล่อยสื่อแสงที่มีความหนาแน่นน้อยกว่าสำหรับวัตถุที่มีความหนาแน่นน้อยกว่า (n1>n2) ลำแสงจะเบี่ยงเบนจากปกติมากขึ้น
ตอนนี้ มาเพิ่มมุมกันเถอะ θ1. เป็นผลให้ช่วงเวลาจะมาถึงเมื่อ θ2 จะเท่ากับ 90o เกิดปรากฏการณ์อัศจรรย์: ลำแสงที่ปล่อยออกมาจากตัวกลางที่มีความหนาแน่นมากขึ้นจะยังคงอยู่ในนั้น นั่นคือเพราะว่าส่วนต่อประสานระหว่างวัสดุโปร่งใสทั้งสองจะกลายเป็นทึบแสง
มุมวิกฤต
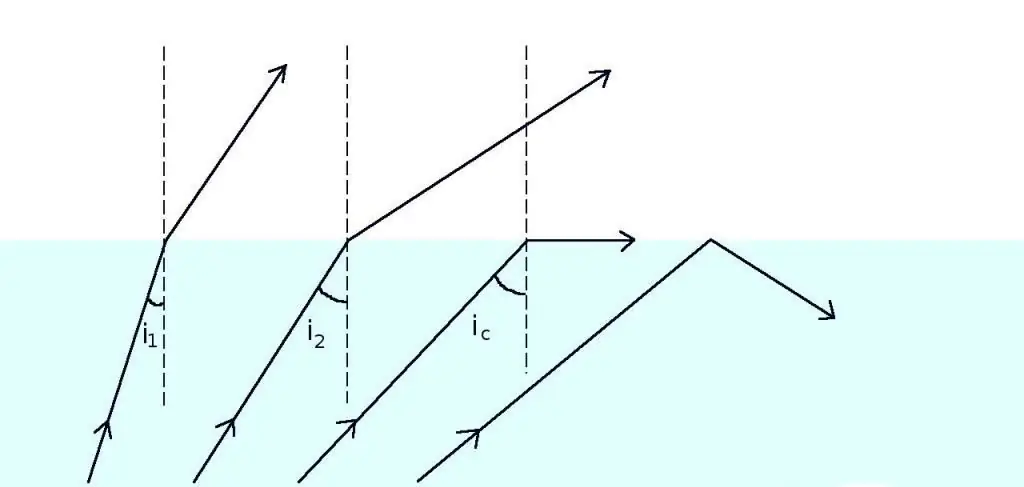
มุม θ1 ซึ่ง θ2=90o เรียกว่า สำคัญสำหรับคู่ของสื่อที่พิจารณา รังสีใดๆ ที่กระทบส่วนต่อประสานในมุมที่มากกว่ามุมวิกฤตจะสะท้อนเข้าไปในตัวกลางแรกอย่างสมบูรณ์ สำหรับมุมวิกฤต θc เราสามารถเขียนนิพจน์ที่ตามมาโดยตรงจากสูตรของ Snell:
sin (θc)=n2 / n1.
ถ้าสื่อที่สองคืออากาศ จากนั้นความเท่าเทียมกันนี้จะลดลงในรูปแบบ:
sin (θc)=1 / n1.
ตัวอย่างเช่น มุมวิกฤตของน้ำคือ:
θc=arcsin (1 / 1, 33)=48, 75o.
หากคุณดำดิ่งลงสู่ก้นสระแล้วมองขึ้นไป คุณจะเห็นท้องฟ้าและเมฆที่ลอยผ่านเหนือศีรษะของคุณเท่านั้น ส่วนที่เหลือของผิวน้ำจะมองเห็นแต่ผนังสระเท่านั้น.
จากเหตุผลข้างต้น เป็นที่ชัดเจนว่า การสะท้อนทั้งหมดไม่ใช่ปรากฏการณ์ที่ย้อนกลับได้ ซึ่งแตกต่างจากการหักเหของแสง มันเกิดขึ้นเมื่อเคลื่อนที่จากตัวกลางที่มีความหนาแน่นมากกว่าไปยังตัวกลางที่มีความหนาแน่นน้อยกว่า แต่ไม่ในทางกลับกัน
ภาพสะท้อนในธรรมชาติและเทคโนโลยี
บางทีเอฟเฟกต์ทั่วไปที่สุดในธรรมชาติ ซึ่งเป็นไปไม่ได้เลยถ้าไม่มีการสะท้อนทั้งหมด ก็คือรุ้งกินน้ำ สีของรุ้งเป็นผลมาจากการกระจายของแสงสีขาวในเม็ดฝน อย่างไรก็ตาม เมื่อรังสีผ่านเข้าไปในละอองเหล่านี้ จะเกิดการสะท้อนภายในแบบเดี่ยวหรือสองครั้ง นั่นคือเหตุผลที่รุ้งปรากฏเป็นสองเท่าเสมอ
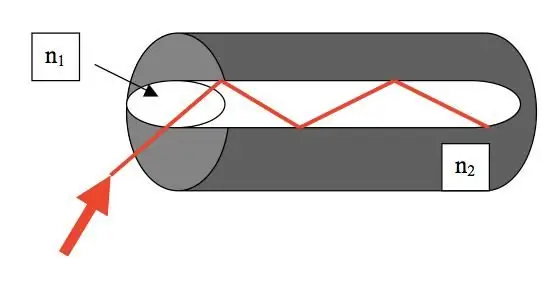
ปรากฏการณ์การสะท้อนภายในทั้งหมดถูกนำมาใช้ในเทคโนโลยีใยแก้วนำแสง ด้วยใยแก้วนำแสงทำให้สามารถส่งคลื่นแม่เหล็กไฟฟ้าได้โดยไม่สูญเสียในระยะทางไกล

