แผนที่ทางภูมิศาสตร์ที่ผู้คนใช้กันมาตั้งแต่สมัยโบราณ ความพยายามครั้งแรกในการพรรณนาพื้นผิวโลกเกิดขึ้นในสมัยกรีกโบราณโดยนักวิทยาศาสตร์เช่น Eratosthenes และ Hipparchus โดยธรรมชาติแล้ว การทำแผนที่ในฐานะวิทยาศาสตร์ได้ก้าวหน้าไปไกลตั้งแต่นั้นเป็นต้นมา แผนที่สมัยใหม่สร้างขึ้นโดยใช้ภาพถ่ายดาวเทียมและเทคโนโลยีคอมพิวเตอร์ ซึ่งแน่นอนว่าช่วยเพิ่มความแม่นยำ อย่างไรก็ตาม ในทุกแผนที่ทางภูมิศาสตร์ มีการบิดเบือนบางประการเกี่ยวกับรูปร่าง มุม หรือระยะทางตามธรรมชาติบนพื้นผิวโลก ธรรมชาติของการบิดเบือนเหล่านี้ และด้วยเหตุนี้ ความแม่นยำของแผนที่จึงขึ้นอยู่กับประเภทของการทำแผนที่ที่ใช้สร้างแผนที่เฉพาะ
แนวคิดของการฉายแผนที่
เรามาดูกันดีกว่าว่าการฉายแผนที่คืออะไรและประเภทใดที่ใช้ในการทำแผนที่สมัยใหม่
การฉายแผนที่เป็นภาพพื้นผิวโลกบนระนาบ มากกว่าคำจำกัดความเชิงลึกทางวิทยาศาสตร์มีลักษณะดังนี้: การฉายภาพการทำแผนที่เป็นวิธีการแสดงจุดบนพื้นผิวโลกบนระนาบบางระนาบ ซึ่งสร้างการพึ่งพาเชิงวิเคราะห์ระหว่างพิกัดของจุดที่สอดคล้องกันของพื้นผิวที่แสดงและพื้นผิวที่แสดง
การฉายแผนที่สร้างขึ้นอย่างไร
การจัดทำแผนที่แบบใดก็ได้เกิดขึ้นในสองขั้นตอน
- ประการแรก พื้นผิวโลกที่ไม่สม่ำเสมอทางเรขาคณิตถูกแมปลงบนพื้นผิวที่ถูกต้องทางคณิตศาสตร์ ซึ่งเรียกว่าพื้นผิวอ้างอิง สำหรับการประมาณที่แม่นยำที่สุด geoid มักถูกใช้ในความสามารถนี้ - วัตถุเรขาคณิตที่ล้อมรอบด้วยผิวน้ำของทะเลและมหาสมุทรทั้งหมดซึ่งเชื่อมต่อถึงกัน (ระดับน้ำทะเล) และมีมวลน้ำเพียงก้อนเดียว ทุกจุดบนพื้นผิว geoid แรงโน้มถ่วงจะถูกนำไปใช้ตามปกติ อย่างไรก็ตาม geoid เช่นเดียวกับพื้นผิวทางกายภาพของดาวเคราะห์ก็ไม่สามารถแสดงออกด้วยกฎทางคณิตศาสตร์เดียวได้ ดังนั้นแทนที่จะเป็น geoid วงรีของการปฏิวัติจึงถูกนำมาใช้เป็นพื้นผิวอ้างอิง ทำให้มีความคล้ายคลึงกันสูงสุดกับ geoid โดยใช้ระดับการบีบอัดและการวางแนวในร่างกายของโลก พวกเขาเรียกร่างกายนี้ว่าทรงโลกหรือทรงรีอ้างอิง และในประเทศต่าง ๆ พวกเขาใช้พารามิเตอร์ต่างกัน
- ประการที่สอง พื้นผิวอ้างอิงที่นำมาใช้ (ทรงรีอ้างอิง) จะถูกถ่ายโอนไปยังระนาบโดยใช้การพึ่งพาเชิงวิเคราะห์อย่างใดอย่างหนึ่งหรืออย่างอื่น เป็นผลให้เราได้ภาพแผนที่แบนของพื้นผิวโลก
การฉายภาพผิดเพี้ยน
อย่านะสงสัยว่าเหตุใดโครงร่างของทวีปจึงแตกต่างกันเล็กน้อยในแผนที่ที่ต่างกัน ในการฉายแผนที่บางส่วน บางส่วนของโลกจะดูใหญ่ขึ้นหรือเล็กลงเมื่อเทียบกับจุดสังเกตบางแห่งมากกว่าส่วนอื่นๆ มันคือทั้งหมดที่เกี่ยวกับการบิดเบือนที่ฉายภาพของโลกไปยังพื้นผิวเรียบ
แต่ทำไมการฉายแผนที่จึงแสดงผลผิดเพี้ยน? คำตอบนั้นค่อนข้างง่าย พื้นผิวทรงกลมไม่สามารถปรับใช้บนระนาบได้ เพื่อหลีกเลี่ยงรอยพับหรือแตกหัก ดังนั้นรูปภาพจากมันจึงไม่สามารถแสดงได้โดยไม่ผิดเพี้ยน
วิธีการรับประมาณการ
การศึกษาการฉายแผนที่ ประเภท และคุณสมบัติ จำเป็นต้องกล่าวถึงวิธีการก่อสร้าง ดังนั้น การฉายแผนที่ทำได้โดยใช้สองวิธีหลัก:
- เรขาคณิต
- วิเคราะห์
วิธีเรขาคณิตเป็นไปตามกฎของเปอร์สเปคทีฟเชิงเส้น โลกของเรามีเงื่อนไขเป็นทรงกลมรัศมีบางส่วน และฉายลงบนพื้นผิวทรงกระบอกหรือทรงกรวย ซึ่งสามารถสัมผัสหรือตัดผ่านได้
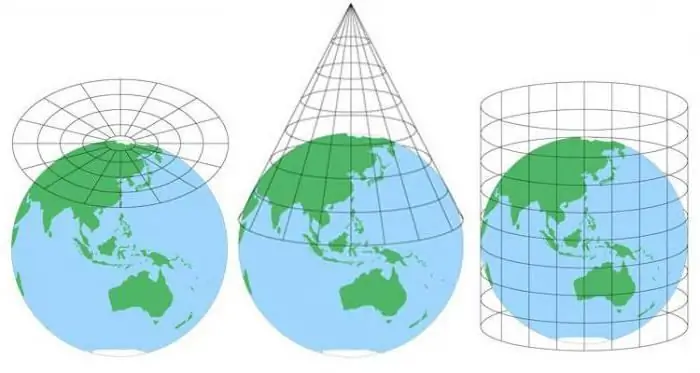
การฉายภาพที่ได้รับในลักษณะนี้เรียกว่าเปอร์สเปคทีฟ ขึ้นอยู่กับตำแหน่งของจุดสังเกตที่สัมพันธ์กับพื้นผิวโลก การฉายภาพเปอร์สเปคทีฟแบ่งออกเป็นประเภท:
- gnomonic หรือศูนย์กลาง (เมื่อมุมมองอยู่ในแนวเดียวกับศูนย์กลางของทรงกลมโลก);
- stereographic (ในกรณีนี้จุดสังเกตตั้งอยู่ที่พื้นผิวอ้างอิง);
- orthographic (เมื่อสังเกตพื้นผิวจากจุดใดๆ นอกทรงกลมของโลก การฉายภาพถูกสร้างขึ้นโดยการย้ายจุดของทรงกลมโดยใช้เส้นคู่ขนานที่ตั้งฉากกับพื้นผิวการแสดงผล)
วิธีการวิเคราะห์สำหรับการสร้างการฉายแผนที่ขึ้นอยู่กับนิพจน์ทางคณิตศาสตร์ที่เชื่อมต่อจุดต่างๆ บนทรงกลมของการอ้างอิงและระนาบการแสดงผล วิธีนี้ใช้งานได้หลากหลายและยืดหยุ่นมากขึ้น ช่วยให้คุณสร้างการคาดคะเนตามลักษณะการบิดเบือนที่กำหนดไว้ล่วงหน้าได้
ประเภทการฉายแผนที่ในภูมิศาสตร์
ในการสร้างแผนที่ทางภูมิศาสตร์ มีการใช้การคาดคะเนของโลกหลายประเภท จำแนกตามเกณฑ์ต่างๆ ในรัสเซียมีการใช้การจำแนกประเภท Kavraysky ซึ่งใช้เกณฑ์สี่ข้อที่กำหนดประเภทหลักของการทำแผนที่ ต่อไปนี้ใช้เป็นพารามิเตอร์การจำแนกลักษณะเฉพาะ:
- ตัวละครเพี้ยน
- รูปแบบการแสดงเส้นพิกัดของตารางปกติ
- ตำแหน่งของจุดขั้วในระบบพิกัดปกติ
- วิธีใช้งาน
แล้วการฉายแผนที่ประเภทใดตามหมวดหมู่นี้
การจำแนกประเภทการฉาย
ต่อไปนี้คือการจำแนกประเภทของการฉายแผนที่พร้อมตัวอย่างตามเกณฑ์หลักข้างต้น
โดยธรรมชาติของการบิดเบือน
ดังที่กล่าวไว้ข้างต้น การบิดเบือนเป็นคุณสมบัติโดยธรรมชาติของการฉายภาพใดๆ ของโลก ลักษณะใด ๆ สามารถบิดเบือนได้พื้นผิว: ความยาว พื้นที่ หรือมุม ตามประเภทของความผิดเพี้ยน พวกเขาแยกแยะ:
- การฉายภาพแบบ Conformal หรือ Conformal โดยที่มุมเอียงและมุมต่าง ๆ จะถูกถ่ายโอนโดยไม่ผิดเพี้ยน ตารางพิกัดในการฉายภาพตามรูปแบบเป็นมุมฉาก ขอแนะนำให้ใช้แผนที่ที่ได้รับในลักษณะนี้เพื่อกำหนดระยะทางในทุกทิศทาง
- การฉายภาพเทียบเท่าหรือเทียบเท่า โดยรักษามาตราส่วนของพื้นที่ไว้ ซึ่งเท่ากับหนึ่ง นั่นคือ พื้นที่จะแสดงโดยไม่มีการบิดเบือน แผนที่ดังกล่าวใช้เพื่อเปรียบเทียบพื้นที่
- การฉายภาพระยะเท่ากันหรือระยะเท่ากัน ในการก่อสร้างที่มีการรักษามาตราส่วนไว้ในทิศทางหลักอันใดอันหนึ่งซึ่งถ่ายเป็นเส้นเดียว
- การคาดคะเนโดยพลการซึ่งสามารถบิดเบือนได้ทุกประเภท
ตามรูปแบบการแสดงเส้นพิกัดของเส้นตารางปกติ
การจัดหมวดหมู่นี้เป็นภาพที่มองเห็นได้ชัดเจนที่สุด ดังนั้น จึงเข้าใจได้ง่ายที่สุด อย่างไรก็ตาม โปรดทราบว่าเกณฑ์นี้ใช้เฉพาะกับการคาดการณ์ที่มุ่งเน้นไปที่จุดสังเกตตามปกติเท่านั้น ดังนั้น ตามลักษณะเฉพาะนี้ การคาดคะเนการทำแผนที่ประเภทต่อไปนี้จึงมีความโดดเด่น:
วงกลม โดยที่เส้นขนานและเส้นเมอริเดียนเป็นวงกลม และเส้นศูนย์สูตรและเส้นเมริเดียนเฉลี่ยของตารางเป็นเส้นตรง การคาดคะเนดังกล่าวใช้เพื่อพรรณนาพื้นผิวโลกโดยรวม ตัวอย่างของการฉายภาพแบบวงกลม ได้แก่ การฉายภาพแบบลากรองจ์ และการฉายภาพแบบกรินเทนตามอำเภอใจ
อาซิมุท ในกรณีนี้ ความคล้ายคลึงกันหมายถึงในรูปแบบของวงกลมที่มีศูนย์กลางและเส้นเมอริเดียนในรูปแบบของมัดของเส้นตรงที่แยกจากจุดศูนย์กลางเรดิอ การฉายภาพแบบเดียวกันนี้ใช้ในตำแหน่งตรงเพื่อแสดงขั้วของโลกที่มีอาณาเขตติดกัน และในตำแหน่งตามขวางเป็นแผนที่ของซีกโลกตะวันตกและตะวันออกที่ทุกคนคุ้นเคยจากบทเรียนภูมิศาสตร์
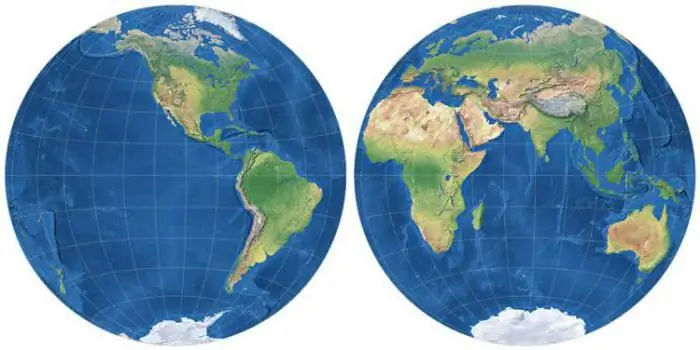
ทรงกระบอก โดยที่เส้นเมอริเดียนและแนวขนานจะแสดงด้วยเส้นตรงที่ตัดกันตามปกติ ดินแดนที่อยู่ติดกับเส้นศูนย์สูตรหรือทอดยาวไปตามละติจูดมาตรฐานบางส่วนจะแสดงที่นี่โดยมีการบิดเบือนน้อยที่สุด
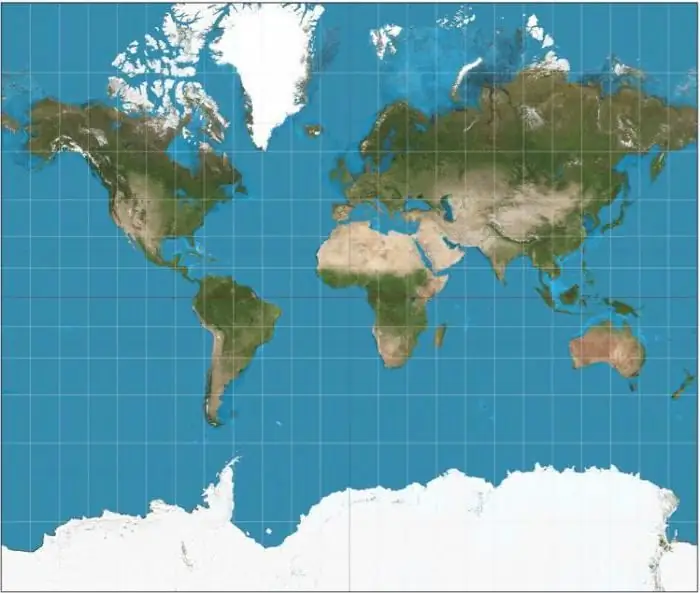
รูปกรวย ซึ่งเป็นตัวแทนของการพัฒนาพื้นผิวด้านข้างของกรวย โดยที่เส้นขนานกันเป็นส่วนโค้งของวงกลมที่มีศูนย์กลางอยู่ที่ด้านบนของกรวย และเส้นเมอริเดียนเป็นตัวนำทางที่แยกออกจากด้านบนของกรวย การคาดคะเนดังกล่าวแสดงภาพอาณาเขตที่อยู่ในละติจูดกลางได้แม่นยำที่สุด
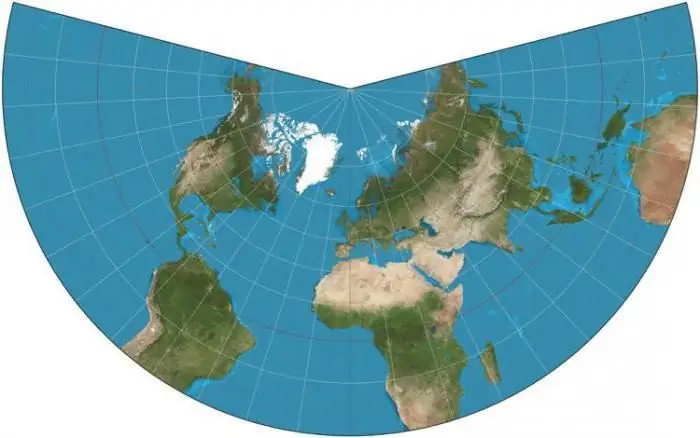
การคาดคะเนเทียมคล้ายกับการคาดคะเนรูปกรวย เฉพาะเส้นเมอริเดียนในกรณีนี้เท่านั้นที่จะแสดงเป็นเส้นโค้งสมมาตรเทียบกับเส้นเมอริเดียนตามแนวแกนที่เป็นเส้นตรงของตาราง
การคาดคะเนรูปทรงกระบอกหลอกคล้ายกับรูปทรงกระบอกเท่านั้น เช่นเดียวกับในเส้นสมมุติฐานรูปกรวย เส้นเมอริเดียนถูกวาดด้วยเส้นโค้งที่สมมาตรกับเส้นเมอริเดียนที่เป็นเส้นตรงแนวแกน ใช้เพื่อพรรณนาถึงทั้งโลก (เช่น รูปวงรี Mollweide, พื้นที่ไซน์ไซดัลเท่ากันซันซัน ฯลฯ).
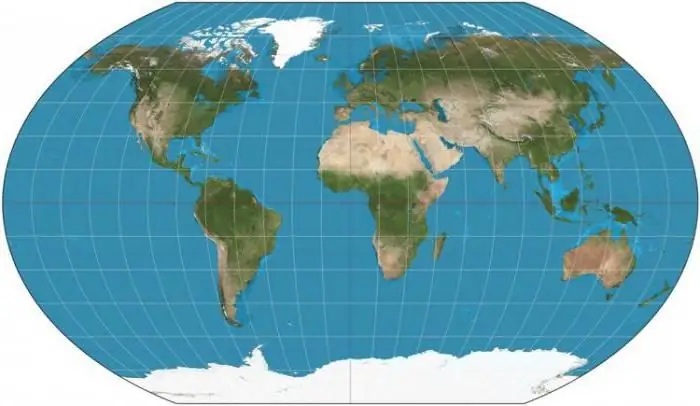
Polyconic โดยที่เส้นขนานถูกวาดเป็นวงกลม โดยจุดศูนย์กลางจะอยู่บนเส้นเมอริเดียนตรงกลางของตารางหรือความต่อเนื่องของมัน เส้นเมอริเดียนจะอยู่ในรูปของเส้นโค้งที่อยู่สมมาตรกับเส้นเมอริเดียนตามแนวแกนที่เป็นเส้นตรง
โดยตำแหน่งของจุดขั้วในระบบพิกัดปกติ
- ขั้วโลกหรือธรรมดา - ขั้วของระบบพิกัดจะเหมือนกับขั้วทางภูมิศาสตร์
- ขวางหรือตามขวาง - ขั้วของระบบปกติอยู่ในแนวเดียวกับเส้นศูนย์สูตร
- เอียงหรือเฉียง - เสาของตารางพิกัดปกติสามารถตั้งอยู่ ณ จุดใดก็ได้ระหว่างเส้นศูนย์สูตรและเสาทางภูมิศาสตร์
ตามวิธีสมัคร
การฉายแผนที่ประเภทต่อไปนี้แยกตามวิธีการใช้งาน:
- แข็ง - การฉายภาพอาณาเขตทั้งหมดบนเครื่องบินเป็นไปตามกฎหมายฉบับเดียว
- หลายเลน - พื้นที่ที่ทำแผนที่ถูกแบ่งออกเป็นโซนละติจูดหลายๆ โซน ซึ่งฉายบนระนาบการแสดงผลตามกฎเดียว แต่มีการเปลี่ยนแปลงพารามิเตอร์สำหรับแต่ละโซน ตัวอย่างของการฉายภาพดังกล่าวคือการฉายภาพ Mufling trapezoidal ซึ่งใช้ในสหภาพโซเวียตสำหรับแผนที่ขนาดใหญ่จนถึงปี 1928
- หลายแง่มุม - อาณาเขตแบ่งออกเป็นหลายโซนตามเงื่อนไขในลองจิจูด การฉายภาพบนเครื่องบินจะดำเนินการตามกฎข้อเดียว แต่มีพารามิเตอร์ต่างกันสำหรับแต่ละโซน (เช่น Gauss-Kruger ฉาย)
- คอมโพสิต เมื่อบางส่วนของดินแดนแมปบนเครื่องบินโดยใช้กฎเกณฑ์อย่างหนึ่ง และพื้นที่ที่เหลืออีกอาณาเขต
ข้อดีของการฉายภาพแบบหลายเลนและแบบหลายมุมคือมีความแม่นยำในการแสดงผลสูงภายในแต่ละโซน อย่างไรก็ตาม ข้อเสียที่สำคัญคือไม่สามารถได้ภาพต่อเนื่อง
แน่นอนว่าทุกการฉายแผนที่สามารถจำแนกได้โดยใช้เกณฑ์แต่ละข้อข้างต้น ดังนั้นการฉายภาพที่มีชื่อเสียงของ Earth Mercator จึงเป็นไปตามรูปแบบ (เชิงมุม) และแนวขวาง (การแปลง) การฉายแบบเกาส์-ครูเกอร์ - รูปทรงกระบอกตามขวางตามขวาง ฯลฯ

