ในส่วนพิเศษของฟิสิกส์ - พลวัต เมื่อพวกเขาศึกษาการเคลื่อนไหวของร่างกาย พวกเขาพิจารณาแรงที่กระทำต่อระบบเคลื่อนที่ หลังสามารถทำงานได้ทั้งด้านบวกและด้านลบ พิจารณาในบทความนี้ว่าแรงเสียดทานคืออะไรและคำนวณอย่างไร
แนวคิดในการทำงานฟิสิกส์
ในทางฟิสิกส์ แนวคิดของ "งาน" แตกต่างจากความคิดทั่วไปของคำนี้ งานถูกเข้าใจว่าเป็นปริมาณทางกายภาพ ซึ่งเท่ากับผลคูณสเกลาร์ของเวกเตอร์แรงและเวกเตอร์การกระจัดของร่างกาย สมมติว่ามีวัตถุบางอย่างที่แรง F¯ กระทำ เนื่องจากไม่มีแรงอื่นมากระทำกับมัน เวกเตอร์การกระจัด l¯ จะตรงกับทิศทางของเวกเตอร์ F¯ ผลคูณสเกลาร์ของเวกเตอร์เหล่านี้ในกรณีนี้จะสอดคล้องกับผลคูณของโมดูล นั่นคือ:
A=(F¯l¯)=Fl.
ค่า A คืองานที่ทำโดยแรง F¯ เพื่อเคลื่อนวัตถุให้ไกล l โดยคำนึงถึงขนาดของค่า F และ l เราพบว่างานวัดเป็นนิวตันต่อเมตร (Nm) ในระบบ SI อย่างไรก็ตาม หน่วยNm มีชื่อเป็นของตัวเอง - เป็นจูล ซึ่งหมายความว่าแนวความคิดในการทำงานเหมือนกับแนวคิดเรื่องพลังงาน กล่าวอีกนัยหนึ่ง ถ้าแรง 1 นิวตันเคลื่อนที่วัตถุ 1 เมตร ค่าพลังงานที่สอดคล้องกันคือ 1 จูล
แรงเสียดทานคืออะไร
การศึกษาคำถามเกี่ยวกับแรงเสียดทานเป็นไปได้ถ้าคุณรู้ว่าเรากำลังพูดถึงแรงประเภทใด การเสียดสีในวิชาฟิสิกส์เป็นกระบวนการที่ป้องกันการเคลื่อนไหวของวัตถุหนึ่งบนพื้นผิวของอีกวัตถุหนึ่งเมื่อพื้นผิวเหล่านี้สัมผัสกัน
หากพิจารณาเฉพาะวัตถุแข็ง แรงเสียดทานสำหรับพวกมันมีสามประเภท:
- พักผ่อน;
- สลิป;
- กลิ้ง
แรงเหล่านี้กระทำระหว่างพื้นผิวที่สัมผัสและมักจะพุ่งเข้าหาการเคลื่อนไหวของร่างกาย
การเสียดสีขณะพักจะป้องกันการเคลื่อนไหวนั้นเอง การเสียดสีแบบเลื่อนจะแสดงขึ้นในกระบวนการเคลื่อนไหว เมื่อพื้นผิวของร่างกายเลื่อนเข้าหากัน และมีการเสียดสีระหว่างตัวที่หมุนบนพื้นผิวและพื้นผิวเอง
ตัวอย่างการกระทำของแรงเสียดทานสถิตคือรถที่เบรกมือบนเนินเขา แรงเสียดทานจากการเลื่อนปรากฏขึ้นเมื่อนักเล่นสกีเคลื่อนที่บนหิมะหรือนักเล่นสเก็ตเคลื่อนตัวบนน้ำแข็ง สุดท้าย แรงเสียดทานจากการหมุนจะทำหน้าที่ในขณะที่ล้อรถเคลื่อนที่ไปตามถนน
แรงสำหรับแรงเสียดทานทั้งสามประเภทคำนวณโดยใช้สูตรต่อไปนี้:
Ft=µtN.
ที่นี่ N คือแรงปฏิกิริยาสนับสนุน µt คือสัมประสิทธิ์แรงเสียดทาน บังคับ Nแสดงขนาดของผลกระทบของการรองรับบนร่างกายในแนวตั้งฉากกับระนาบของพื้นผิว สำหรับพารามิเตอร์ µt จะวัดจากการทดลองสำหรับวัสดุถูแต่ละคู่ เช่น ไม้ ไม้ เหล็ก-หิมะ และอื่นๆ ผลลัพธ์ที่วัดได้จะถูกรวบรวมไว้ในตารางพิเศษ
สำหรับแรงเสียดทานแต่ละค่าสัมประสิทธิ์ µt มีค่าของตัวเองสำหรับคู่ของวัสดุที่เลือก ดังนั้น ค่าสัมประสิทธิ์แรงเสียดทานสถิตจึงมากกว่าค่าสัมประสิทธิ์แรงเสียดทานแบบเลื่อนหลายสิบเปอร์เซ็นต์ ในทางกลับกัน สัมประสิทธิ์การกลิ้งจะมีขนาดน้อยกว่าการเลื่อน 1-2 คำสั่ง
งานแรงเสียดทาน
ตอนนี้เมื่อทำความคุ้นเคยกับแนวคิดของงานและประเภทของความขัดแย้งแล้ว คุณสามารถไปที่หัวข้อของบทความได้โดยตรง ลองพิจารณาเรียงลำดับแรงเสียดทานทุกประเภทและดูว่าพวกมันทำงานอย่างไร
เริ่มด้วยแรงเสียดทานสถิตกัน ประเภทนี้แสดงออกเมื่อร่างกายไม่เคลื่อนไหว เนื่องจากไม่มีการเคลื่อนที่ เวกเตอร์การกระจัด l¯ จึงเท่ากับศูนย์ อันหลังหมายถึงงานของแรงเสียดทานสถิตเท่ากับศูนย์เช่นกัน
การเสียดสีเลื่อนโดยนิยาม ทำหน้าที่เฉพาะเมื่อร่างกายเคลื่อนที่ในอวกาศเท่านั้น เนื่องจากแรงเสียดทานประเภทนี้มักจะมุ่งไปที่การเคลื่อนไหวของร่างกาย นั่นหมายความว่ามันทำงานด้านลบ ค่าของ A สามารถคำนวณได้โดยใช้สูตร:
A=-Ftl=-µtNl.
การเลื่อนแรงเสียดทานมุ่งเป้าไปที่การเคลื่อนไหวของร่างกายช้าลง จากการทำงานนี้ พลังงานกลของร่างกายจะเปลี่ยนเป็นความร้อน

การเสียดสีเหมือนการไถลก็เกี่ยวข้องกับการเคลื่อนไหวของร่างกายเช่นกัน แรงเสียดทานจากการกลิ้งทำงานด้านลบ ทำให้การหมุนเริ่มต้นของร่างกายช้าลง เนื่องจากเรากำลังพูดถึงการหมุนของร่างกาย จึงสะดวกที่จะคำนวณมูลค่าของแรงกระทำผ่านการทำงานของโมเมนตัม สูตรที่สอดคล้องกันเขียนเป็น:
A=-Mθ โดยที่ M=FtR.
ที่นี่ θ คือมุมของการหมุนของร่างกายอันเป็นผลมาจากการหมุน R คือระยะห่างจากพื้นผิวถึงแกนหมุน (รัศมีวงล้อ)
ปัญหาเกี่ยวกับแรงเสียดทานจากการเลื่อน
เป็นที่ทราบกันดีว่ามีท่อนไม้อยู่บนขอบระนาบไม้เอียง เครื่องบินเอียงไปที่ขอบฟ้าเป็นมุม 40o โดยรู้ว่าค่าสัมประสิทธิ์แรงเสียดทานจากการเลื่อนเท่ากับ 0.4 ความยาวของระนาบคือ 1 เมตร และมวลของแท่งเหล็กเท่ากับ 0.5 กก. จึงจำเป็นต้องหาค่าแรงเสียดทานจากการเลื่อน
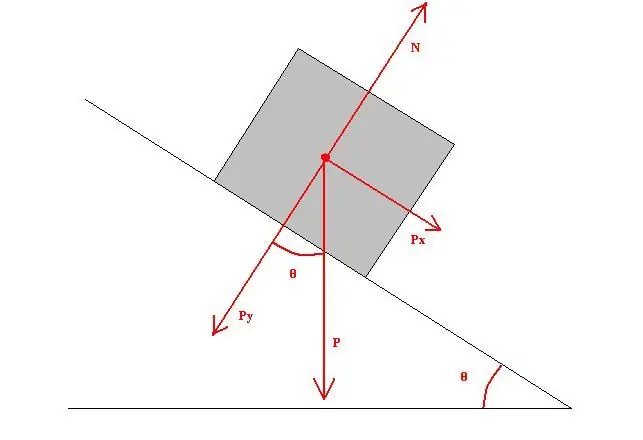
คำนวณแรงเสียดทานจากการเลื่อน. เท่ากับ:
Ft=mgcos(α)µt=0.59.81cos(40 o)0, 4=1.5 N.
จากนั้นงานที่เกี่ยวข้อง A จะเป็น:
A=-Ftl=-1.51=-1.5 J.
ปัญหาความฝืดในการกลิ้ง
เป็นที่ทราบกันดีว่าล้อหมุนไปตามถนนเป็นระยะทางหนึ่งและหยุดลง เส้นผ่านศูนย์กลางของล้อคือ 45 ซม. จำนวนรอบของล้อก่อนหยุดคือ 100 โดยคำนึงถึงค่าสัมประสิทธิ์การหมุนเท่ากับ 0.03 จำเป็นต้องค้นหาว่าแรงเสียดทานของแรงเสียดทานทำงานเท่ากับเท่าใด น้ำหนักล้อ 5 กก.

ขั้นแรก มาคำนวณโมเมนต์ความเสียดทานการกลิ้งกัน:
M=FtR=µtmgD/2=0.0359, 81 0, 45/2=0, 331 Nm.
หากจำนวนรอบของวงล้อคูณด้วย 2pi เรเดียน เราก็จะได้มุมการหมุนของวงล้อ θ แล้วสูตรการทำงานคือ
A=-Mθ=-M2pin.
โดยที่ n คือจำนวนรอบ แทนที่โมเมนต์ M และจำนวน n จากเงื่อนไข เราจะได้งานที่ต้องการ: A=- 207.87 J.




