สัมประสิทธิ์ความสอดคล้อง: ตัวอย่างการคำนวณและสูตร ค่าสัมประสิทธิ์ความสอดคล้องคืออะไร?

2024 ผู้เขียน: Angel Austin | [email protected]. แก้ไขล่าสุด: 2024-01-02 17:57

เมื่อการตรวจสอบโดยเพื่อน เช่น การประเมินความสามารถในการแข่งขันของผลิตภัณฑ์ การประมวลผลข้อมูลทางสถิติก็เป็นสิ่งจำเป็นเช่นเดียวกับงานทางวิทยาศาสตร์ใดๆ ขั้นหลังเริ่มต้นด้วยการพิจารณาความสอดคล้องของความคิดเห็นของผู้เชี่ยวชาญ การแสดงออกทางตัวเลขคือสัมประสิทธิ์ความสอดคล้อง

ทำไมเราต้องมีการประเมินฉันทามติจากผู้เชี่ยวชาญ

การประเมินนี้มีความจำเป็น ก่อนอื่น เนื่องจากความคิดเห็นของผู้เชี่ยวชาญอาจแตกต่างกันอย่างมากในพารามิเตอร์ที่ประมาณการ ในขั้นต้น การประเมินจะดำเนินการโดยการจัดอันดับตัวชี้วัดและกำหนดสัมประสิทธิ์นัยสำคัญ (น้ำหนัก) ให้กับพวกเขา การจัดอันดับที่ไม่สอดคล้องกันส่งผลให้สัมประสิทธิ์เหล่านี้ไม่น่าเชื่อถือทางสถิติ ความคิดเห็นของผู้เชี่ยวชาญที่มีจำนวนที่ต้องการ (มากกว่า 7-10) ควรเผยแพร่ตามกฎหมายปกติ

แนวคิดของสัมประสิทธิ์ความสอดคล้อง

งั้น. ความสม่ำเสมอคือความสอดคล้อง ค่าสัมประสิทธิ์คือปริมาณที่ไม่มีมิติซึ่งแสดงอัตราส่วนของการกระจายตัวต่อการกระจายตัวสูงสุดในกรณีทั่วไป มาสรุปแนวคิดเหล่านี้กัน

ค่าสัมประสิทธิ์ความสอดคล้องคือตัวเลขตั้งแต่ 0 ถึง 1 แสดงความสอดคล้องของความคิดเห็นของผู้เชี่ยวชาญเมื่อจัดอันดับคุณสมบัติบางอย่าง ยิ่งค่านี้ใกล้ 0 มากเท่าใด ความสอดคล้องจะถือว่าต่ำลงเท่านั้น หากค่าสัมประสิทธิ์นี้น้อยกว่า 0.3 ถือว่าความคิดเห็นของผู้เชี่ยวชาญไม่สอดคล้องกัน เมื่อค่าสัมประสิทธิ์อยู่ในช่วง 0.3 ถึง 0.7 จะถือว่าความสอดคล้องเป็นค่าเฉลี่ย ค่าที่มากกว่า 0.7 ถือว่ามีความสม่ำเสมอสูง

การใช้งาน

เมื่อทำการวิจัยทางสถิติ สถานการณ์อาจเกิดขึ้นซึ่งวัตถุอาจมีลักษณะเฉพาะไม่ใช่สองลำดับ ซึ่งถูกประมวลผลทางสถิติโดยใช้สัมประสิทธิ์ความสอดคล้อง แต่หลายลำดับ ซึ่งจัดอันดับโดยผู้เชี่ยวชาญที่มีระดับเดียวกัน ความเป็นมืออาชีพในบางพื้นที่

ความสอดคล้องของการจัดอันดับที่ดำเนินการโดยผู้เชี่ยวชาญจะต้องกำหนดเพื่อยืนยันความถูกต้องของสมมติฐานที่ผู้เชี่ยวชาญทำการวัดที่ค่อนข้างแม่นยำ ซึ่งช่วยให้เกิดการจัดกลุ่มต่างๆ ในกลุ่มผู้เชี่ยวชาญ ซึ่งส่วนใหญ่กำหนดโดยปัจจัยมนุษย์ เช่น ความแตกต่างในมุมมอง แนวคิด โรงเรียนวิทยาศาสตร์ต่างๆ ธรรมชาติของกิจกรรมทางวิชาชีพ เป็นต้น

คำอธิบายโดยย่อของวิธีการจัดอันดับ ข้อดีและข้อเสีย

เมื่อจัดอันดับ จะใช้วิธีจัดอันดับ สาระสำคัญของมันอยู่ในความจริงที่ว่าแต่ละคุณสมบัติของวัตถุได้รับการจัดอันดับเฉพาะของตัวเอง นอกจากนี้ ผู้เชี่ยวชาญแต่ละคนที่รวมอยู่ในกลุ่มผู้เชี่ยวชาญ ตำแหน่งนี้จะได้รับมอบหมายส่งผลให้จำเป็นต้องประมวลผลข้อมูลเหล่านี้เพื่อระบุความสอดคล้องของความคิดเห็นของผู้เชี่ยวชาญ กระบวนการนี้ดำเนินการโดยการคำนวณค่าสัมประสิทธิ์ความสอดคล้อง

ข้อได้เปรียบหลักของวิธีการจัดอันดับคือความง่ายในการใช้งาน

ข้อเสียหลักของวิธีนี้คือ:

• จำนวนเล็กน้อยของวัตถุการจัดอันดับ เนื่องจากเมื่อจำนวนของพวกเขาเกิน 15-20 เป็นเรื่องยากที่จะกำหนดคะแนนการจัดอันดับตามวัตถุประสงค์
• จากการใช้วิธีนี้ คำถามที่ว่าวัตถุที่ศึกษาอยู่ห่างจากกันอย่างมีนัยสำคัญยังคงเปิดอยู่

เมื่อใช้วิธีนี้ ต้องคำนึงว่าการให้คะแนนนั้นขึ้นอยู่กับรูปแบบความน่าจะเป็นบางประเภท ดังนั้นต้องใช้ด้วยความระมัดระวังเมื่อพิจารณาจากขอบเขต

สัมประสิทธิ์อันดับความสอดคล้องของเคนดัลล์

ใช้เพื่อกำหนดความสัมพันธ์ระหว่างคุณสมบัติเชิงปริมาณและเชิงคุณภาพที่แสดงลักษณะวัตถุที่เป็นเนื้อเดียวกันและจัดอันดับตามหลักการเดียวกัน

สัมประสิทธิ์นี้ถูกกำหนดโดยสูตร:

t=2S/(n(n-1)), โดยที่

S - ผลรวมของความแตกต่างระหว่างจำนวนลำดับและจำนวนการผกผันในฟีเจอร์ที่สอง

n - จำนวนการสังเกต

อัลกอริธึมการคำนวณ:

• ค่า x จะเรียงลำดับจากน้อยไปมากหรือมากไปน้อย
• ค่า y ถูกจัดเรียงตามลำดับที่สอดคล้องกับค่า x.
• สำหรับอันดับที่ต่อเนื่องกันของ y ให้กำหนดว่าค่าอันดับที่สูงกว่านั้นตามมากี่ค่า รวมกันแล้ววัดความสอดคล้องของลำดับของอันดับใน x และ y
• ในทำนองเดียวกัน จำนวนอันดับของ y ที่มีค่าต่ำกว่าจะถูกคำนวณ ซึ่งรวมเข้าด้วยกัน
• เพิ่มจำนวนอันดับที่มีค่าสูงกว่าและจำนวนอันดับที่มีค่าต่ำกว่าส่งผลให้ค่า S.

สัมประสิทธิ์นี้แสดงความสัมพันธ์ระหว่างสองตัวแปร และในกรณีส่วนใหญ่เรียกว่าสัมประสิทธิ์สหสัมพันธ์อันดับเคนดัลล์ การพึ่งพาอาศัยกันดังกล่าวสามารถแสดงเป็นภาพกราฟิกได้

การหาสัมประสิทธิ์

ทำอย่างไร? หากจำนวนของคุณสมบัติหรือปัจจัยที่มีการจัดอันดับมากกว่า 2 ค่าสัมประสิทธิ์ความสอดคล้องจะถูกใช้ ซึ่งโดยพื้นฐานแล้ว คือตัวแปรหลายระดับของความสัมพันธ์ของอันดับ

ระวัง. การคำนวณค่าสัมประสิทธิ์ความสอดคล้องนั้นขึ้นอยู่กับอัตราส่วนของการเบี่ยงเบนของผลรวมกำลังสองของอันดับจากผลรวมเฉลี่ยของกำลังสองของอันดับ คูณด้วย 12 ถึงกำลังสองของผู้เชี่ยวชาญ คูณด้วยผลต่างระหว่างลูกบาศก์ของตัวเลข ของสิ่งของและจำนวนสิ่งของ

อัลกอริธึมการคำนวณ

เพื่อให้เข้าใจว่าเลข 12 มาจากไหนในตัวเศษของสูตรการคำนวณ มาดูอัลกอริธึมการกำหนดกันดีกว่า

สำหรับแต่ละบรรทัดที่มียศของผู้เชี่ยวชาญบางคน ผลรวมของอันดับจะถูกคำนวณ ซึ่งเป็นค่าสุ่ม

ค่าสัมประสิทธิ์ความสอดคล้องถูกกำหนดโดยทั่วไปเป็นอัตราส่วนของการประมาณค่าความแปรปรวน (D) ต่อค่าสูงสุดของค่าประมาณความแปรปรวน(D_{max). ให้เรากำหนดคำจำกัดความของปริมาณเหล่านี้อย่างต่อเนื่อง}

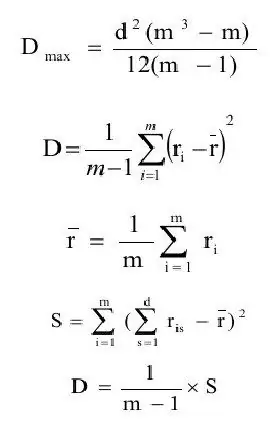
ที่ไหน r_{avg - ประมาณการที่คาดไว้;}

m - จำนวนวัตถุ

การแทนที่สูตรผลลัพธ์ที่สัมพันธ์กับ D เป็น D_{max เราจะได้สูตรสุดท้ายสำหรับสัมประสิทธิ์ความสอดคล้อง:}

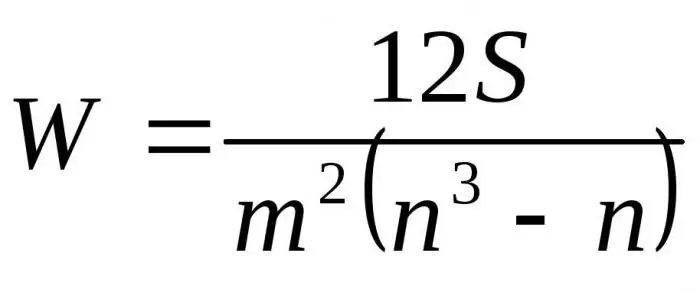
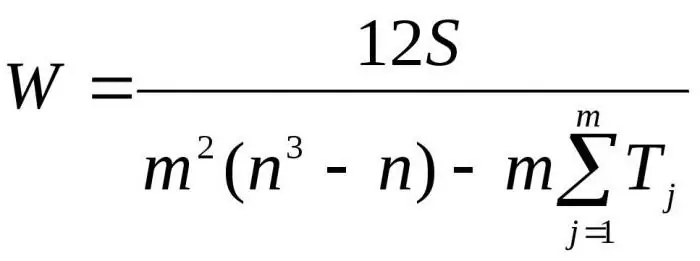
นี่คือจำนวนผู้เชี่ยวชาญ n คือจำนวนวัตถุ

สูตรแรกใช้เพื่อกำหนดปัจจัยที่สอดคล้องกันหากไม่มีอันดับที่เกี่ยวข้อง สูตรที่สองจะใช้หากมีอันดับที่เกี่ยวข้อง

ดังนั้น การคำนวณค่าสัมประสิทธิ์ความสอดคล้องสิ้นสุดลง อะไรต่อไป? ค่าที่ได้รับจะถูกประเมินหานัยสำคัญโดยใช้สัมประสิทธิ์เพียร์สันโดยการคูณสัมประสิทธิ์นี้ด้วยจำนวนผู้เชี่ยวชาญและจำนวนองศาอิสระ (m-1) เกณฑ์ผลลัพธ์จะถูกเปรียบเทียบกับค่าในตาราง และถ้าค่าแรกเกินค่าสุดท้าย พวกเขาจะพูดถึงความสำคัญของสัมประสิทธิ์ภายใต้การศึกษา

ในกรณีของอันดับที่เกี่ยวข้องกัน การคำนวณเกณฑ์ของเพียร์สันจะค่อนข้างซับซ้อนและดำเนินการตามอัตราส่วนต่อไปนี้: (12S)/(d(m²+ ม.)-(1/(m-1))x(T_s1 +T_s2 +T_sn)

ตัวอย่าง

สมมติว่าวิธีการของผู้เชี่ยวชาญประเมินความสามารถในการแข่งขันของเนยที่ขายในเครือข่ายค้าปลีก ให้เรายกตัวอย่างการคำนวณค่าสัมประสิทธิ์ความสอดคล้องกัน ก่อนประเมินความสามารถในการแข่งขัน จำเป็นต้องจัดอันดับผู้บริโภคก่อนคุณสมบัติของผลิตภัณฑ์นี้ที่เกี่ยวข้องกับการประเมิน สมมติว่าคุณสมบัติเหล่านี้จะเป็นดังนี้: รสชาติและกลิ่น ความสม่ำเสมอและลักษณะที่ปรากฏ สี บรรจุภัณฑ์และการติดฉลาก ปริมาณไขมัน ชื่อทางการค้า ผู้ผลิต ราคา

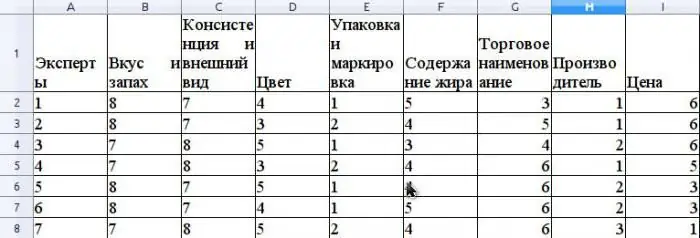
สมมติว่ากลุ่มผู้เชี่ยวชาญประกอบด้วยผู้เชี่ยวชาญ 7 คน รูปแสดงผลการจัดอันดับคุณสมบัติเหล่านี้

ค่าเฉลี่ยของ r คำนวณเป็นค่าเฉลี่ยเลขคณิตและจะเท่ากับ 31.5 ในการหา S ให้รวมผลต่างกำลังสองระหว่าง r_{is และค่าเฉลี่ย r ตามสูตร ด้านบน และกำหนดว่าค่าของ S คือ 1718}

คำนวณสัมประสิทธิ์ความสอดคล้องโดยใช้สูตรโดยไม่ใช้อันดับที่เกี่ยวข้อง (อันดับจะสัมพันธ์กันหากที่ปรึกษาผู้เชี่ยวชาญคนเดียวกันมีอันดับเดียวกันสำหรับคุณสมบัติต่างกัน)

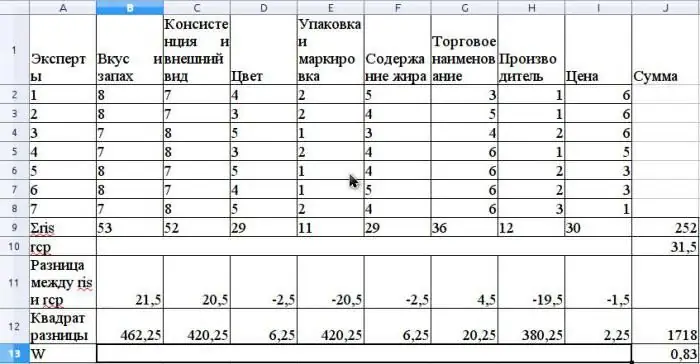
ค่าสัมประสิทธิ์นี้จะเท่ากับ 0.83 ซึ่งบ่งชี้ว่าผู้เชี่ยวชาญเห็นพ้องต้องกันอย่างเข้มแข็ง

ตรวจสอบความสำคัญโดยใช้การทดสอบ Pearson:

7 x 0.83 x (8-1)=40.7.

การทดสอบตารางของเพียร์สันที่ระดับนัยสำคัญ 1% คือ 18.5 และที่ 5% - 14.1.

ตัวอย่างแสดงให้เห็นถึงความเรียบง่ายและการเข้าถึงของการคำนวณสำหรับผู้ที่รู้พื้นฐานการคำนวณทางคณิตศาสตร์ เพื่อบรรเทาพวกเขาใช้แบบฟอร์มสเปรดชีต

สรุป

ดังนั้น สัมประสิทธิ์ความสอดคล้องแสดงความสอดคล้องของความคิดเห็นของผู้เชี่ยวชาญหลายคน ยิ่งห่างจาก 0 และใกล้ 1 มากเท่าใด ความคิดเห็นก็จะยิ่งสอดคล้องกันมากขึ้น สัมประสิทธิ์เหล่านี้ต้องได้รับการยืนยันโดยการคำนวณเกณฑ์ของเพียร์สัน