ลักษณะเด่นของแผนที่ในบริเวณนี้มักถูกแยกออกมาต่างหาก นี่คือความแม่นยำของมาตราส่วน ในบทความเราจะวิเคราะห์สิ่งที่แนวคิดนี้ซ่อนอยู่ในตัวมันเอง เราจะพิจารณาด้วยว่ามาตราส่วนโดยทั่วไปเป็นอย่างไรเราจะอธิบายลักษณะพันธุ์หลัก มาวิเคราะห์ว่าแนวคิดของ "ความถูกต้องของกราฟิก" เกี่ยวข้องกับหัวข้อการสนทนาของเราอย่างไร
นี่คืออะไร
มาตราส่วนเป็นการชี้แจงที่สำคัญที่แสดงว่าแต่ละเส้นที่วาดบนภาพวาด แบบแปลน นั้นน้อยกว่าหรือมากกว่าขนาดจริงของวัตถุที่แสดง คำชี้แจงดังกล่าวจะนำเสนอในเอกสารการวาดและแผนที่ทั้งแบบตัวเลขและแบบกราฟิก
ขนาดของแผน ความแม่นยำของมาตราส่วน - แนวคิดที่สามารถพบได้ในหลายพื้นที่:
- การทำแผนที่
- ออกแบบ
- มาตร.
- รูปภาพ
- การสร้างโมเดล
- การเขียนโปรแกรม
- คณิตศาสตร์
- โรงหนัง
บางส่วนของแอปพลิเคชันเหล่านี้ คุณสมบัติของพวกเขา เราจะพิจารณาในบทความต่อไป
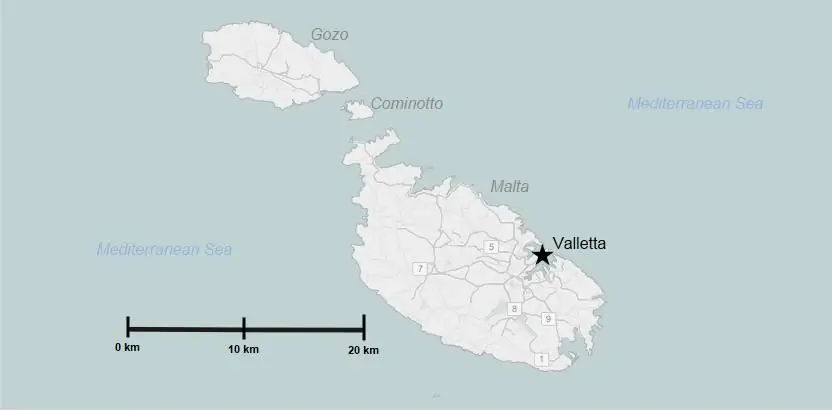
ความแม่นยำในการปรับขนาด
และตอนนี้คำจำกัดความของแนวคิดหลัก ความแม่นยำของมาตราส่วน - ส่วนหนึ่งของระยะห่างระหว่างเส้นแนวนอน ซึ่งจะหมายถึง 0.1 มม. บนภาพวาด เหตุใดจึงเลือกค่านี้
0, 1 มม. เป็นที่ยอมรับที่นี่เนื่องจากเป็นส่วนที่เล็กที่สุดที่สามารถแยกแยะได้ด้วยสายตามนุษย์ในภาพโดยไม่ต้องใช้อุปกรณ์เครื่องมืออุปกรณ์พิเศษ
มาดูตัวอย่างที่เป็นรูปธรรมกันเถอะ ให้ 1:10000 ความแม่นยำของมาตราส่วนจะอยู่ที่ 1 ม. ตามลำดับ มาวิเคราะห์รายละเอียดเพิ่มเติมกัน:
- 1 ซม. บนแผนผังหรือรูปภาพคือ 10,000 ซม. (หรือ 100 ม.) บนภูมิประเทศจริง
- ในภาพขนาด 1 มม. 1,000 ซม. (หรือ 10 ม.)
- 0, 1mm คือ 100cm (หรือ 1m) บนภูมิประเทศจริง
ดังนั้นจึงง่ายต่อการกำหนดความแม่นยำสูงสุดของมาตราส่วน นี่คือระยะห่างของพื้นผิวจริง เท่ากับ 0.1 มม. บนแผนที่ - ส่วนต่ำสุดที่บุคคลสามารถแยกแยะได้
ความเที่ยงตรงของกราฟิก
แล้วมาทำความคุ้นเคยกับกราฟิกที่แม่นยำของตาชั่งกัน นี่เป็นอีกหนึ่งคุณลักษณะที่สำคัญเมื่อใช้แผนและแผนที่
ความถูกต้องของกราฟิกสัมพันธ์กับความละเอียด "และ" ของสายตามนุษย์ ในทางกลับกันก็ทำให้ "จี" ดังนั้น G=u.
นั่นคือ ถ้ามุม "และ" ระหว่างเวกเตอร์เป็นสองจุด "B" และ "L" เมื่อผู้สังเกตที่มีระดับการมองเห็นปกติเป็น "G" ขึ้นไป จะมองเห็นได้ เป็นสองจุด หากมุมนี้กับแนวคิดของความละเอียดน้อยกว่า "G" แล้ว "L" และ "B" จะถูกมองว่าเป็นหนึ่งเดียวdot.
ควรทำความคุ้นเคยกับคำจำกัดความของความแม่นยำของมาตราส่วนในตัวอย่างที่เฉพาะเจาะจงจะดีที่สุด สมมติว่ามีผู้ตรวจสอบแผนที่จากระยะที่ดีที่สุด "b" เท่ากับ 35 ซม. ค่าของ G=u ตอนนี้ คุณจำเป็นต้องกำหนดระยะทางที่เล็กที่สุด (นั่นคือ ความแม่นยำของกราฟิก) ระหว่าง "B" และ "L" ซึ่งผู้สังเกตจะยังคงถูกมองว่าเป็นจุดสองจุดที่แตกต่างกัน นี่คือการคำนวณ:
1 - คือ! - 1/3438 x 350 mm=0.1 mm.
1/3438 คือค่าของมุม u=r ซึ่งในกรณีนี้แสดงเป็นเรเดียน (3438' คือจำนวนนาทีในหน่วยเรเดียน)
ดังนั้น ค่าเอาต์พุต 0.1 มม. คือความแม่นยำของกราฟิกของแผนหรือแผนที่
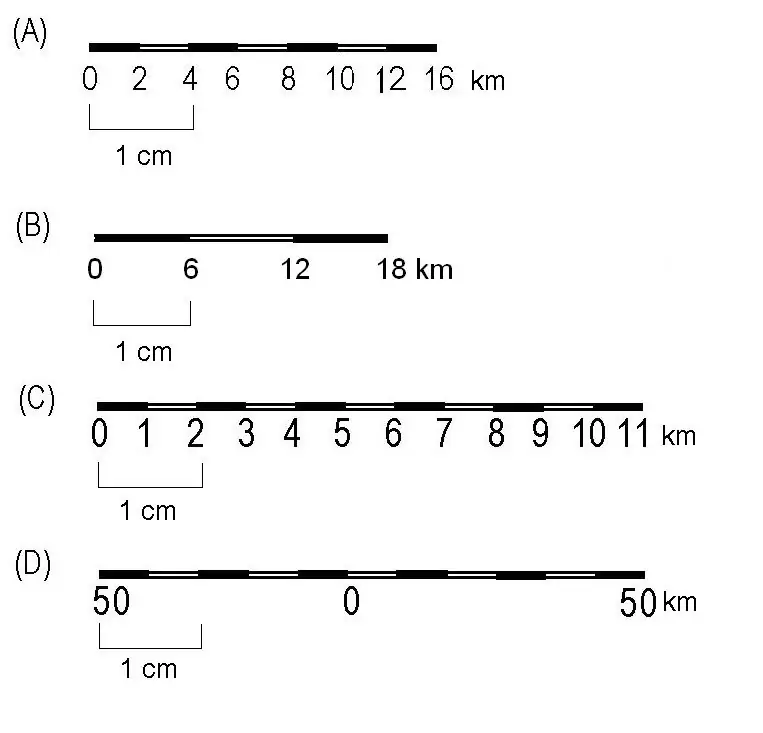
ความเชื่อมโยงของแนวคิด
ตอนนี้เรามาดูกันว่าคำข้างต้นเกี่ยวข้องกับคำหลักอย่างไร ความแม่นยำของมาตราส่วนคืออย่างที่เราจำได้ ระยะห่างบนพื้นผิวโลก ซึ่งเท่ากับ 0.1 มม. บนเอกสาร
คุณสามารถหาสูตร:
T=gM=0.1 M มม.
ถอดรหัสองค์ประกอบ:
- T - ความแม่นยำของมาตราส่วน
- M เป็นตัวหารมาตราส่วน
- r=0.1 มม. - ความแม่นยำของกราฟิก
จากที่นี่เราสามารถอนุมานการตีความที่เกี่ยวข้องได้ ความแม่นยำของมาตราส่วน - ความแม่นยำแบบกราฟิก ซึ่งแสดงเป็นมาตราส่วนของแผนที่หรือแผน และผลเป็นอย่างไร? ความแม่นยำของกราฟิกจะกลายเป็นค่าคงที่ (0.1 มม.) สำหรับเครื่องชั่งที่มีอยู่ทั้งหมด
ดังนั้น ความแม่นยำของมาตราส่วนจะเปลี่ยนไปตามไปด้วย จะยิ่งสูง คอมไพเลอร์ก็ยิ่งเลือกมาตราส่วน
และตอนนี้เราจะจัดการกับคุณสมบัติของลักษณะเช่นมาตราส่วนในด้านต่าง ๆ ของการใช้งาน
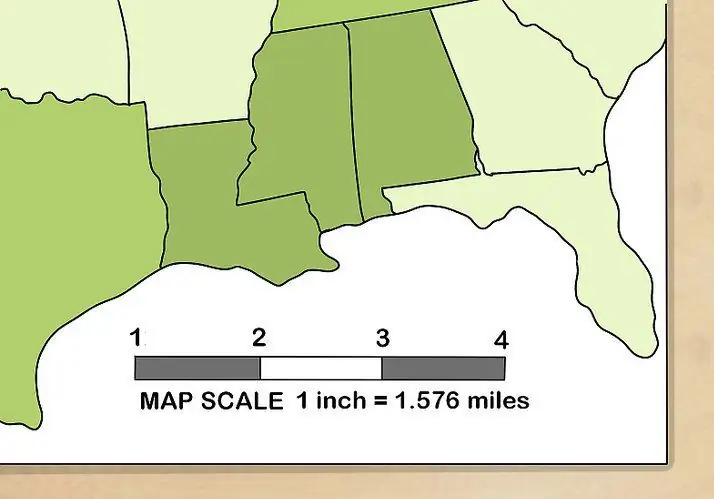
การออกแบบ มาตรวิทยา และการทำแผนที่
เรารู้ดีว่าความแม่นยำของมาตราส่วน "500" หมายถึงอะไร - 1:500 ให้เราพิจารณาว่ารูปแบบใดบ้างที่เป็นแบบฉบับสำหรับสาขาการออกแบบ การทำแผนที่ และมาตรวิทยา:
- สเกลตัวเลข. ตัวบ่งชี้ถูกเขียนเป็นเศษส่วน ตัวเศษจะเป็นหนึ่ง และตัวส่วนจะลดระดับการฉายภาพลงบนแผนที่ ตัวอย่างเช่น ลองใช้มาตราส่วน 1:5,000 กัน หมายความว่า 1 ซม. บนแผน แผนที่คือ 5,000 ซม. (หรือ 50 ม.) บนภูมิประเทศจริง ดังนั้นจะมีสเกลที่ใหญ่กว่าที่มีตัวส่วนน้อยกว่า ดังนั้น 1:1,000 จะมากกว่า 1:20,000
- ชื่อสเกล. คอมไพเลอร์ของแผนที่กำหนดในเอกสารว่าระยะทางบนภูมิประเทศจริงเท่ากับ 1 ซม. บนแผนในเอกสาร นี่คือตัวอย่าง: "มี 1,000 กิโลเมตรใน 1 เซนติเมตร" หรือเรียกสั้นๆ ว่า "1 ซม.=100 กม."
- สเกลกราฟิก. ในทางกลับกันก็จะแบ่งออกเป็นแนวขวางและเชิงเส้น เราจะวิเคราะห์แยกกัน

กราฟิกหลากหลายหมวดหมู่
ความแม่นยำของมาตราส่วน - มาตราส่วนขวางคืออะไร? มาทำความรู้จักกับคุณสมบัติกัน:
- เชิงเส้น. มาตราส่วนกราฟิกดังกล่าวบนแผนที่จะแสดงเป็นไม้บรรทัด ซึ่งจะแบ่งออกเป็นส่วนต่างๆ จริง
- ขวาง. นี่คือมาตราส่วนกราฟิกที่แสดงเป็นโนโมแกรมโครงสร้างขึ้นอยู่กับสัดส่วนของส่วนของเส้นคู่ขนานที่ตัดกับด้านข้างของมุม มาตราส่วนนี้ใช้สำหรับการวัดความยาวของเส้นบนแผนได้แม่นยำยิ่งขึ้น พวกเขาใช้วิธีนี้: พวกเขาวัดความยาวในบรรทัดล่างของมาตราส่วนตามขวางที่กำหนดเพื่อให้ปลายด้านขวาอยู่ที่ระยะทางทั้งหมด (OM) และด้านซ้ายเกิน 0 หากในกรณีนี้ขาซ้ายคือ ระหว่างส่วนที่สิบตามลำดับของส่วนด้านซ้าย (จาก 0) จากนั้นผู้เชี่ยวชาญจะยกขาทั้งสองของมิเตอร์ขึ้น จนกว่าขาซ้ายของมิเตอร์จะอยู่ที่จุดตัดของเส้นแนวนอนและแนวขวางใดๆ แต่ขาขวาก็ควรอยู่บนเส้นแนวนอนเช่นกัน ซีดีขั้นต่ำที่นี่คือ 0.2 มม. ดังนั้นความแม่นยำที่เล็กที่สุดคือ 0.1 มม.
ชุดของขนาดภาพในการออกแบบ
เรารู้แล้วว่าความเที่ยงตรงของมาตราส่วน 1:500 หมายถึงอะไร แต่ในกรณีใดที่คอมไพเลอร์เลือกมัน? มาวิเคราะห์คำถามนี้กัน:
- ลดขนาดลง. ดังนั้นจึงใช้ในกรณีที่จำเป็นต้องพรรณนาวัตถุบนแผนซึ่งเป็นภูมิประเทศที่เกินพื้นที่อย่างมีนัยสำคัญ หากคอมไพเลอร์หันไปใช้การออกแบบแผนแม่บทที่มีขนาดใหญ่โดยเฉพาะเขาจะต้องใช้มาตราส่วนต่อไปนี้: 1:2,000, 1:5,000, 1:10,000, 1:20,000, 1:25,000, 1:50,000
- ขนาดจริง. หากคุณต้องการพรรณนาถึงวัตถุในแผน "ตามที่เป็นอยู่" ให้อ้างอิงมาตราส่วน "หนึ่งต่อหนึ่ง" ดังนั้น ความยาวจริง 1 ซม. ที่นี่จะสอดคล้องกับความยาว 1 ซม. บนแผนผัง
- ตาชั่งกำลังขยาย จำเป็นในกรณีที่จำเป็นต้องวาดภาพวัตถุที่มีขนาดเล็กเกินไปในแผนสำหรับความคุ้นเคยโดยละเอียดกับลักษณะที่ปรากฏของอุปกรณ์
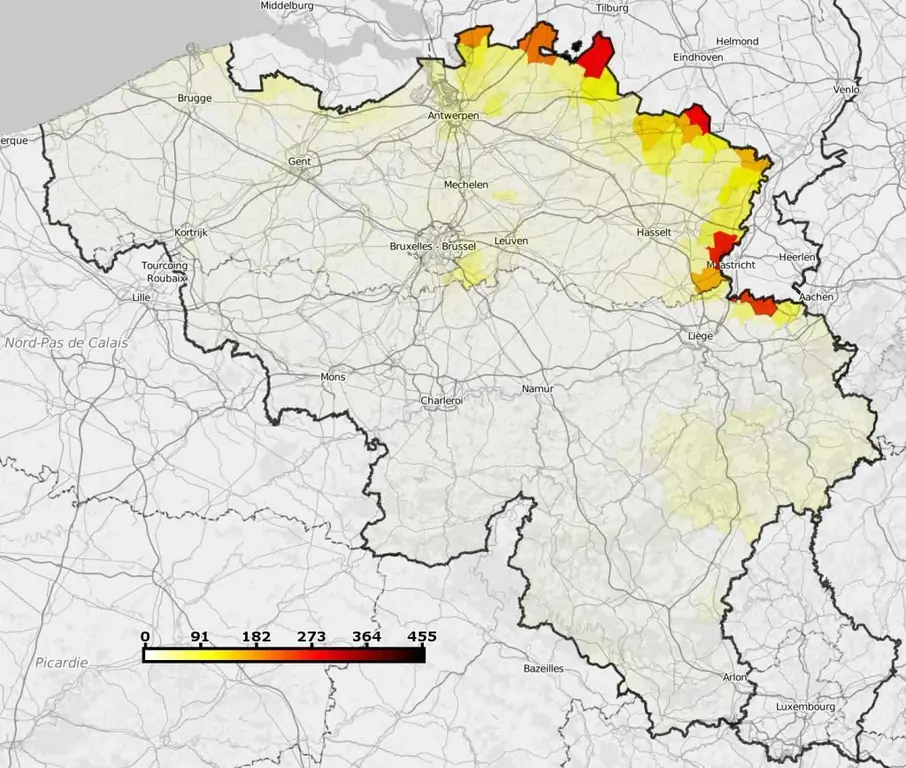
ในรูป
แน่นอน ความแม่นยำของมาตราส่วน 1:10,000 นั้นสัมพันธ์กับการทำแผนที่มากกว่า แต่สิ่งนี้ใช้ได้กับโลกแห่งการถ่ายภาพเช่นกัน มาตราส่วนในที่นี้หมายถึงอัตราส่วนของขนาดที่เรียกว่ามิติเชิงเส้นของภาพที่ได้จากเมทริกซ์อัลตราไวซ์หรือบนฟิล์มถ่ายภาพกับขนาดของการฉายภาพของโซนการฉายภาพที่สอดคล้องกันบนระนาบที่ตั้งฉากกับกล้อง
มีช่างภาพที่วัดมาตราส่วนเป็นอัตราส่วนของขนาดของวัตถุจริงต่อขนาดบนหน้าจอ กระดาษภาพถ่าย หรือสื่ออื่นๆ แต่วิธีที่ถูกต้องในการกำหนดมาตราส่วนในภาพถ่ายนั้นขึ้นอยู่กับบริบทที่ใช้ภาพเท่านั้น
ในการถ่ายภาพ มาตราส่วนก็มีความสำคัญเช่นกันเมื่อคำนวณความลึกของวัตถุที่ปรากฎอย่างคมชัด ช่องว่าง ทุกวันนี้ ผู้เชี่ยวชาญสามารถเข้าถึงเครื่องชั่งได้หลากหลายตั้งแต่ขนาดเล็กมาก (ใช้เมื่อถ่ายภาพวัตถุท้องฟ้าที่อยู่ห่างไกล) ไปจนถึงขนาดใหญ่มาก (โดยไม่ต้องใช้อุปกรณ์เสริมออปติคัลพิเศษ เช่น วันนี้ สามารถรับภาพขนาด 10:1 ได้).
ในที่นี้ การถ่ายภาพมาโครถือว่าถ่ายที่อัตราส่วน 1:1 แล้ว (และใหญ่กว่าด้วย) แต่ด้วยการแพร่กระจายของกล้องดิจิตอลคอมแพค การถ่ายภาพมาโครจึงถูกเรียกว่าสไตล์เมื่อวางเลนส์ไว้ใกล้กับวัตถุมากเกินไป เมื่อพิจารณาจากนิยามคลาสสิกแล้วการตีความดังกล่าวจะไม่ถูกต้อง
ในโมเดล
สำหรับการสร้างแบบจำลองม้านั่ง (หรือมาตราส่วน) แต่ละประเภท จะมีการกำหนดมาตราส่วนของตัวเอง ประกอบด้วยเครื่องชั่งหลายตัวซึ่งมีการลดลงในระดับหนึ่ง ที่น่าสนใจสำหรับการสร้างแบบจำลองแต่ละประเภท (ทางรถไฟ รถยนต์ การสร้างแบบจำลองเรือ ยุทโธปกรณ์ทางทหาร การสร้างแบบจำลองเครื่องบิน) มีชุดมาตราส่วนที่สร้างขึ้นในอดีตซึ่งไม่ตัดกับแบบอื่น
นี่มาตราส่วนคำนวณโดยสูตรง่ายๆ:
L / M=X.
ถอดรหัส:
- L - พารามิเตอร์ดั้งเดิม
- M - ขนาดที่จำเป็นสำหรับการทำงาน
- X คือค่าที่ต้องการ
อยู่ในโปรแกรม
ในบริเวณนี้ มาตราส่วนเวลาที่เรียกว่ามีความสำคัญ มาดูกันว่ามันคืออะไร
ในระบบปฏิบัติการการแบ่งปันเวลา การให้ "เรียลไทม์" กับงานเฉพาะเป็นสิ่งสำคัญมาก มันแตกต่างตรงที่การประมวลผลเหตุการณ์ภายนอกดำเนินไปโดยไม่มีความล่าช้าหรือช่องว่างเพิ่มเติม ที่นี่อีกหนึ่งแนวคิดจะมีความสำคัญ - "มาตราส่วนเวลาจริง" แต่ควรเข้าใจว่าไม่มีความสัมพันธ์โดยตรงกับมาตราส่วนบนแผนที่ นี่เป็นเพียงข้อตกลงเชิงคำศัพท์
ในเทคโนโลยีภาพยนตร์
ในเทคโนโลยีภาพยนตร์ ความแม่นยำของมาตราส่วนเวลาก็มีความสำคัญเช่นกัน หลังหมายถึงตัวบ่งชี้เชิงปริมาณของการชะลอตัวหรือเร่งการเคลื่อนไหวซึ่งจะเท่ากับอัตราส่วนของอัตราเฟรมการฉายต่ออัตราการยิง
ลองคิดดูง่ายๆตัวอย่าง. อัตราเฟรมการฉายสำหรับการถ่ายภาพยนตร์คือ 24 fps ถ่ายทำพร้อมกัน "ด้วยความเร็ว" 72 เฟรม / วินาที มาตราส่วนเวลาในกรณีนี้คือ 1:3
แล้วจะมีความหมายเช่นไร เช่น 2:1? ซึ่งเร็วเป็นสองเท่าของกระแสมาตรฐานของสิ่งที่เกิดขึ้นบนหน้าจอ
ในวิชาคณิตศาสตร์
ในพื้นที่นี้ มาตราส่วนหมายถึงความสัมพันธ์เชิงเส้นของสองมิติ นอกจากนี้ ในหลายพื้นที่ที่ใช้ได้จริง นี่จะเป็นอัตราส่วนของขนาดรูปภาพกับขนาดจริงของรูปภาพ
ในทางคณิตศาสตร์ มาตราส่วนคืออัตราส่วนของระยะทางใดๆ บนแผนที่กับระยะทางจริงบนภูมิประเทศจริง หากเราดูตัวอย่าง ก็เหมือนกับในการเขียนแผนที่ สมมติว่า 1:100,000,000 ดังนั้น 1 ซม. ในภาพคือ 100,000 ซม. ในความเป็นจริง นั่นคือพันเมตรหรือหนึ่งกิโลเมตร
มาตราส่วนเป็นลักษณะเฉพาะที่ใช้กันอย่างแพร่หลาย นี่เป็นองค์ประกอบมาตรฐานและสำคัญในการพัฒนาแผน ภาพวาดของวัตถุ แผนที่ของพื้นที่ ใช้ในการออกแบบ ใน geodesy การทำแผนที่ เกี่ยวข้องกับการถ่ายภาพ เทคโนโลยีภาพยนตร์ การเขียนโปรแกรม และคณิตศาสตร์ มันมีลักษณะเฉพาะเป็นหลักโดยความแม่นยำ - อัตราส่วนของระยะทางจริงกับระยะทางที่ยอมรับบนแผนที่






