ยิ่งนักเรียนอายุมากขึ้นก็ยิ่งต้องการความรวดเร็วในการแก้ปัญหาง่ายๆ ไม่มีเวลามากในการสอบเพื่อแก้ปัญหาตัวอย่างง่าย ๆ หรือปัญหาเป็นเวลานาน วิธีหาเส้นทแยงมุมของสี่เหลี่ยมจัตุรัสอย่างรวดเร็วและง่ายดาย สิ่งนี้สอนให้เด็กตั้งแต่เกรดแปด บทความนี้แสดงสองวิธี - วิธีหนึ่งยาวขึ้น อีกวิธีหนึ่งเร็วกว่า
วิธีคำนวณเส้นทแยงมุมของสี่เหลี่ยมจัตุรัส
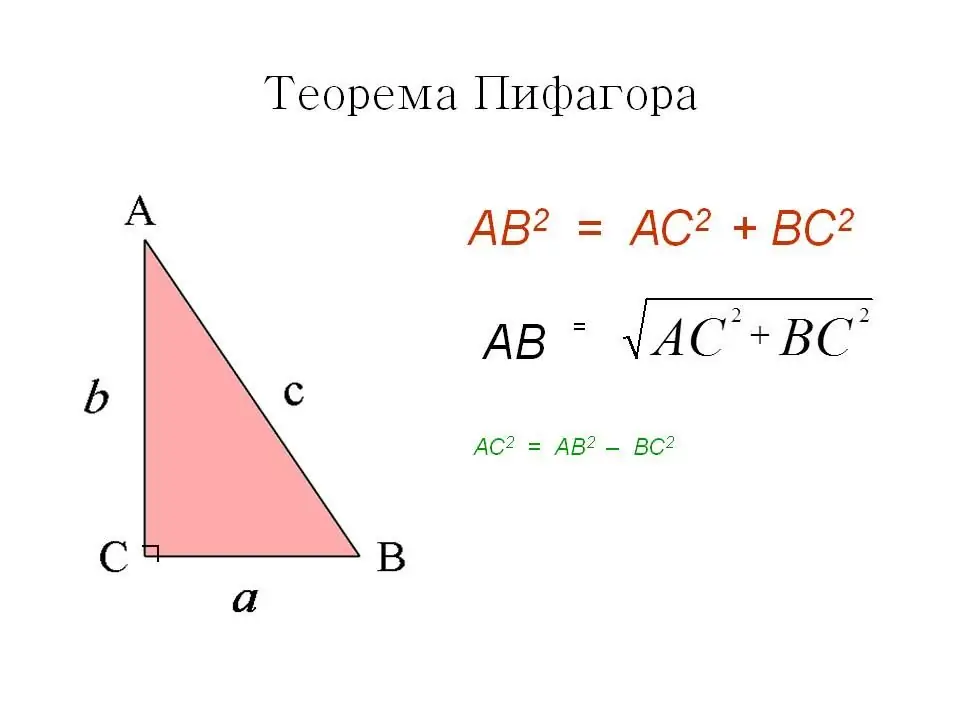
วิธีแรกคือทฤษฎีบทพีทาโกรัสที่คุ้นเคยและคุ้นเคย ในรูปสี่เหลี่ยมจัตุรัส มุมทั้งหมดอยู่ในมุมที่ถูกต้อง ซึ่งหมายความว่าเส้นทแยงมุมแบ่งออกเป็นสามเหลี่ยมมุมฉากสองรูปเท่ากันและเป็นด้านตรงข้ามมุมฉาก ตามทฤษฎีบทพีทาโกรัส สี่เหลี่ยมจัตุรัสของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของขา

วิธีที่สองคือสูตรง่ายๆ ที่ไม่เหมือนใครสำหรับกำลังสอง และคุณแค่ต้องจำไว้ อย่างที่คุณทราบ ทุกด้านของสี่เหลี่ยมจัตุรัสเท่ากันทุกด้าน และด้วยเหตุนี้นักคณิตศาสตร์จึงคำนวณสูตรต่อไปนี้เพื่อหาเส้นทแยงมุม: มันเท่ากับผลคูณของด้านและรากของสอง
แน่นอน ดีที่สุดคือจำสูตรสำหรับความยาวของเส้นทแยงมุมของสี่เหลี่ยมจัตุรัสแล้วใช้เสมอ เพราะมันเร็วและสะดวกกว่ามาก สิ่งนี้รู้สึกได้โดยเฉพาะอย่างยิ่งเมื่อแก้ปัญหาในรูปแบบตัวอักษร ซึ่งแทนที่จะใช้นิพจน์รากขนาดใหญ่ทั้งหมด คุณสามารถแก้ปัญหาได้ด้วยผลิตภัณฑ์เพียงชิ้นเดียว
ตัวอย่าง
เอา เช่น สี่เหลี่ยม 6 คูณ 6 นั่นคือ มีด้านเท่ากับหกเซนติเมตร
ตามวิธีแรก: ให้เส้นทแยงมุมเป็น C และด้านเป็น A
แล้วเราจะได้ C=√A^2+A^2 หรือ C=√2A^2.
เขียนเป็นตัวเลข: С=√36 + 36 เราได้ √72 ซึ่งก็คือ 3√8 หรือ 6√2.
แล้วลองหาเส้นทแยงมุมกัน แต่วิธีที่ 2 C=A√2 หรือในรูปตัวเลข: 6√2
ตอนนี้คุณจะเห็นได้ว่าวิธีที่สองนั้นเร็ว ง่ายขึ้น และที่สำคัญที่สุด - มีประสิทธิภาพมากขึ้น โดยเฉพาะอย่างยิ่งในปัญหาง่าย ๆ เช่นนั้น เพราะทุกนาทีมีค่าในการสอบ!
คุณสมบัติอื่นๆ ของเส้นทแยงมุม
นอกจากจะรู้วิธีหาเส้นทแยงมุมของสี่เหลี่ยมแล้ว คุณยังต้องรู้คุณสมบัติของพวกมันด้วย หลักๆคือ:
- เส้นทแยงมุมเท่ากันและจุดตัดแบ่งครึ่ง
- พวกมันก่อตัวเป็นมุมฉากเมื่อพวกมันตัดกัน
- แบ่งสี่เหลี่ยมจัตุรัสออกเป็นสามเหลี่ยมเท่าๆ กัน
สรุป
คำถามเกี่ยวกับวิธีการนับเส้นทแยงมุมของสี่เหลี่ยมมักจะถามโดยนักเรียนที่พลาดหัวข้อนี้ที่โรงเรียน อย่างไรก็ตาม ทุกคนควรรู้กฎพื้นฐานของคณิตศาสตร์เช่นนี้! เป็นที่พึงปรารถนาที่จะแก้ปัญหาโดยเร็วที่สุดและต้องใช้ความรู้เกี่ยวกับสูตรย่อ ทั้งหมดนี้เป็นเรื่องง่ายและง่ายมาก แต่ในขณะเดียวกันก็เป็นพื้นฐานที่จำเป็นสำหรับการแก้ปัญหาที่ซับซ้อนมากขึ้นในอนาคต และส่วนสำคัญของฐานนี้คือสี่เหลี่ยม

