ฟิสิกส์: สูตรความต้านทานและกฎของโอห์ม

2024 ผู้เขียน: Angel Austin | [email protected]. แก้ไขล่าสุด: 2024-01-02 17:57

กฎของโอห์มคือกฎพื้นฐานของวงจรไฟฟ้า ในขณะเดียวกันก็ช่วยให้เราสามารถอธิบายปรากฏการณ์ทางธรรมชาติได้มากมาย ตัวอย่างเช่น เราสามารถเข้าใจได้ว่าทำไมไฟฟ้าถึงไม่ "ตี" นกที่เกาะอยู่บนสายไฟ สำหรับฟิสิกส์ กฎของโอห์มมีความสำคัญอย่างยิ่ง หากปราศจากความรู้ของเขา มันจะเป็นไปไม่ได้ที่จะสร้างวงจรไฟฟ้าที่เสถียรหรือจะไม่มีอุปกรณ์อิเล็กทรอนิกส์เลย

การพึ่งพา I=I(U) และมูลค่าของมัน

ประวัติการค้นพบความต้านทานของวัสดุนั้นเกี่ยวข้องโดยตรงกับลักษณะเฉพาะของแรงดันไฟในปัจจุบัน มันคืออะไร? ลองใช้วงจรที่มีกระแสไฟคงที่และพิจารณาองค์ประกอบต่างๆ เช่น โคมไฟ ท่อแก๊ส ตัวนำโลหะ กระติกน้ำอิเล็กโทรไลต์ เป็นต้น

การเปลี่ยนแรงดันไฟฟ้า U (มักเรียกว่า V) ที่จ่ายให้กับองค์ประกอบที่เป็นปัญหา เราจะติดตามการเปลี่ยนแปลงในความแรงของกระแส (I) ที่ไหลผ่าน เป็นผลให้เราได้รับการพึ่งพาแบบฟอร์ม I \u003d I (U) ซึ่งเรียกว่า "ลักษณะแรงดันไฟฟ้าขององค์ประกอบ" และเป็นตัวบ่งชี้โดยตรงของสมบัติทางไฟฟ้า

V/A ลักษณะเฉพาะอาจแตกต่างกันไปตามองค์ประกอบต่างๆ รูปแบบที่ง่ายที่สุดได้มาจากการพิจารณาตัวนำโลหะซึ่งทำโดย Georg Ohm (1789 - 1854)

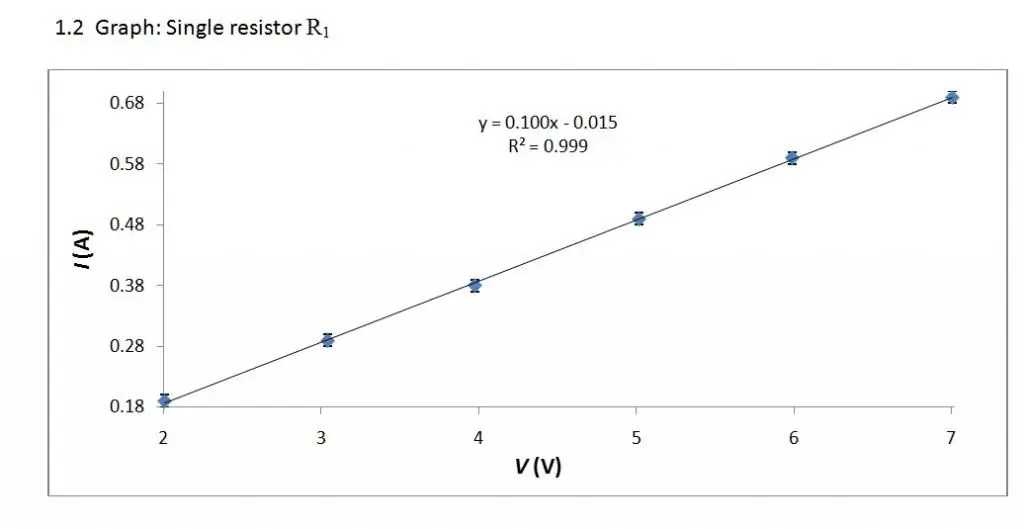
ลักษณะโวลต์-แอมแปร์เป็นความสัมพันธ์เชิงเส้น ดังนั้น กราฟของมันคือเส้นตรง

กฎหมายในรูปแบบที่ง่ายที่สุด

การวิจัยของโอห์มเกี่ยวกับลักษณะแรงดันกระแสของตัวนำพบว่ากำลังกระแสภายในตัวนำโลหะเป็นสัดส่วนกับความต่างศักย์ที่ปลาย (I ~ U) และแปรผกผันกับสัมประสิทธิ์บางอย่าง นั่นคือ ผม ~ 1/ร. ค่าสัมประสิทธิ์นี้เรียกว่า "ความต้านทานตัวนำ" และหน่วยวัดความต้านทานไฟฟ้าคือโอห์มหรือ V/A

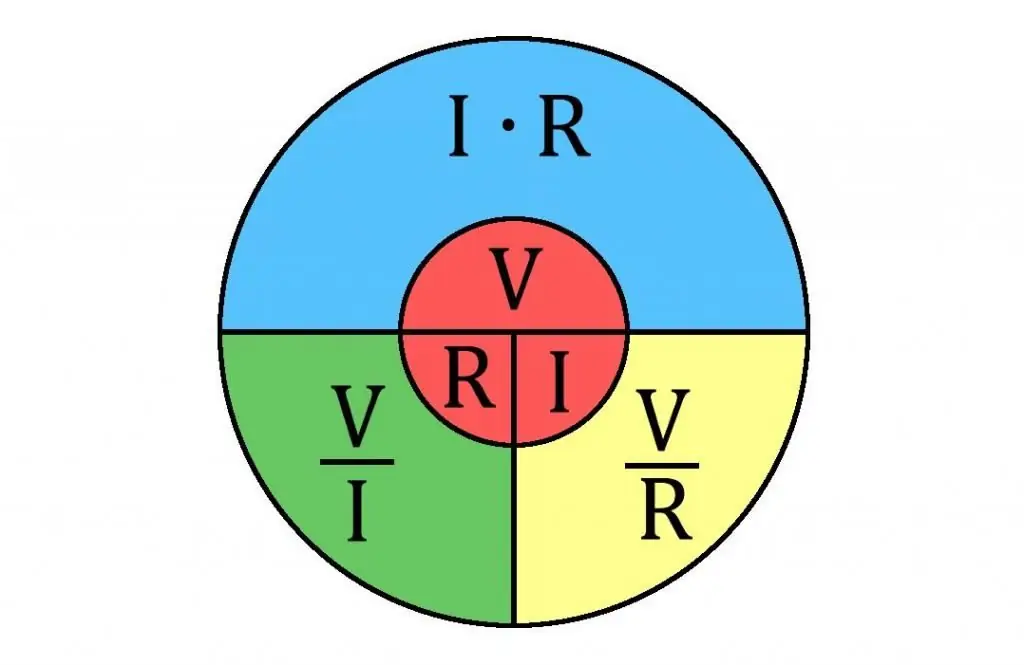
สิ่งหนึ่งที่ควรทราบ กฎของโอห์มมักใช้ในการคำนวณความต้านทานในวงจร

คำกฎหมาย

กฎของโอห์มกล่าวว่าความแรงกระแส (I) ของส่วนเดียวของวงจรเป็นสัดส่วนกับแรงดันไฟฟ้าในส่วนนี้และเป็นสัดส่วนผกผันกับความต้านทาน

ควรสังเกตว่าในรูปแบบนี้ กฎหมายยังคงเป็นความจริงสำหรับส่วนที่เป็นเนื้อเดียวกันของห่วงโซ่เท่านั้น เป็นเนื้อเดียวกันคือส่วนหนึ่งของวงจรไฟฟ้าที่ไม่มีแหล่งกำเนิดกระแส วิธีการใช้กฎของโอห์มในวงจรที่ไม่เป็นเนื้อเดียวกันจะกล่าวถึงด้านล่าง

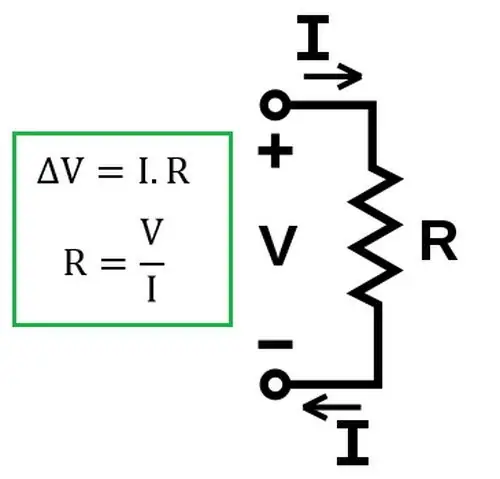
ต่อมาได้มีการทดลองกันว่ากฎหมายยังคงใช้ได้สำหรับการแก้ปัญหาอิเล็กโทรไลต์ในวงจรไฟฟ้า

ความหมายทางกายภาพของการต่อต้าน

ความต้านทานเป็นสมบัติของวัสดุ สาร หรือสื่อที่ป้องกันไม่ให้กระแสไฟฟ้าไหลผ่าน ในเชิงปริมาณความต้านทาน 1 โอห์มหมายความว่าในตัวนำที่มีแรงดันไฟฟ้า 1 V ที่ปลายกระแสไฟฟ้า 1 A สามารถผ่านได้

ความต้านทานไฟฟ้า

จากการทดลอง พบว่าความต้านทานของกระแสไฟฟ้าของตัวนำนั้นขึ้นอยู่กับขนาดของมัน ความยาว ความกว้าง ความสูง และรูปร่างของมัน (ทรงกลม ทรงกระบอก) และวัสดุที่ใช้ทำ ดังนั้น สูตรสำหรับความต้านทาน ตัวอย่างเช่น ของตัวนำทรงกระบอกที่เป็นเนื้อเดียวกันจะเป็น: R \u003d pl / S.

ถ้าในสูตรนี้เราใส่ s=1 m2 และ l=1 m แล้ว R จะเท่ากับ p จากที่นี่ หน่วยวัดสำหรับสัมประสิทธิ์ความต้านทานของตัวนำใน SI คำนวณ - นี่คือโอห์มม.

ในสูตรความต้านทาน p คือสัมประสิทธิ์ความต้านทานที่กำหนดโดยคุณสมบัติทางเคมีของวัสดุที่ใช้ทำตัวนำ

เพื่อพิจารณารูปแบบอนุพันธ์ของกฎของโอห์ม เราต้องพิจารณาแนวคิดเพิ่มเติมอีกสองสามข้อ

ความหนาแน่นกระแส

อย่างที่คุณทราบ กระแสไฟฟ้าเป็นการสั่งการอย่างเข้มงวดของอนุภาคที่มีประจุ ตัวอย่างเช่น ในโลหะ สารพาหะในปัจจุบันคืออิเล็กตรอน และในการนำก๊าซคือไอออน

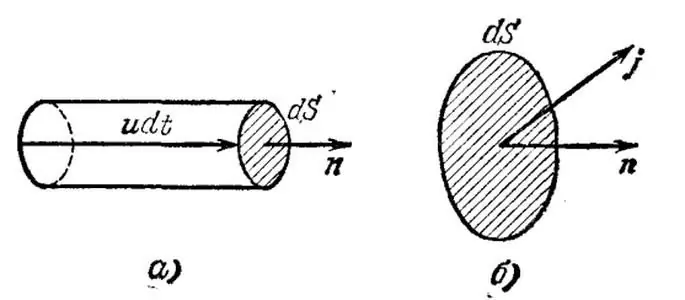
พิจารณากรณีเล็กน้อยเมื่อผู้ให้บริการปัจจุบันทั้งหมดเป็นเนื้อเดียวกัน - ตัวนำโลหะ ให้เราแยกปริมาตรขนาดเล็กอย่างไม่สิ้นสุดในตัวนำนี้ออกทางจิตใจและแสดงความเร็วเฉลี่ยของอิเล็กตรอนในปริมาตรที่กำหนดโดยคุณ นอกจากนี้ ให้ n แสดงถึงความเข้มข้นของผู้ให้บริการปัจจุบันต่อปริมาตรหน่วย

ตอนนี้ เรามาวาดพื้นที่อนันต์ dS ตั้งฉากกับเวกเตอร์ u และสร้างทรงกระบอกเล็กที่มีความสูง udt ตามความเร็ว โดยที่ dt หมายถึงเวลาที่ตัวพาความเร็วปัจจุบันทั้งหมดที่อยู่ในปริมาตรที่พิจารณาจะผ่านไป ผ่านพื้นที่ dS.

ในกรณีนี้ ประจุเท่ากับ q=neudSdt จะถูกถ่ายโอนโดยอิเล็กตรอนผ่านพื้นที่ โดยที่ e คือประจุของอิเล็กตรอน ดังนั้น ความหนาแน่นของกระแสไฟฟ้าจึงเป็นเวกเตอร์ j=neu ซึ่งแสดงถึงปริมาณประจุที่ถ่ายโอนต่อหน่วยเวลาผ่านพื้นที่หนึ่งหน่วย

ข้อดีอย่างหนึ่งของนิยามความแตกต่างของกฎของโอห์มคือคุณมักจะผ่านได้โดยไม่ต้องคำนวณความต้านทาน

ค่าไฟ. ความแรงของสนามไฟฟ้า

ความแรงของสนามพร้อมกับประจุไฟฟ้าเป็นพารามิเตอร์พื้นฐานในทฤษฎีไฟฟ้า ในเวลาเดียวกัน แนวคิดเชิงปริมาณของพวกเขาสามารถหาได้จากการทดลองง่ายๆ ที่มีให้สำหรับเด็กนักเรียน

เพื่อความเรียบง่าย เราจะพิจารณาสนามไฟฟ้าสถิต นี่คือสนามไฟฟ้าที่ไม่เปลี่ยนแปลงตามเวลา สนามดังกล่าวสามารถสร้างขึ้นได้ด้วยประจุไฟฟ้าที่อยู่กับที่

ยังต้องเสียค่าทดสอบเพื่อจุดประสงค์ของเรา เราจะใช้ร่างกายที่มีประจุ - เล็กมากจนไม่สามารถก่อให้เกิดได้การรบกวนใด ๆ (การแจกจ่ายค่าใช้จ่าย) ในวัตถุโดยรอบ

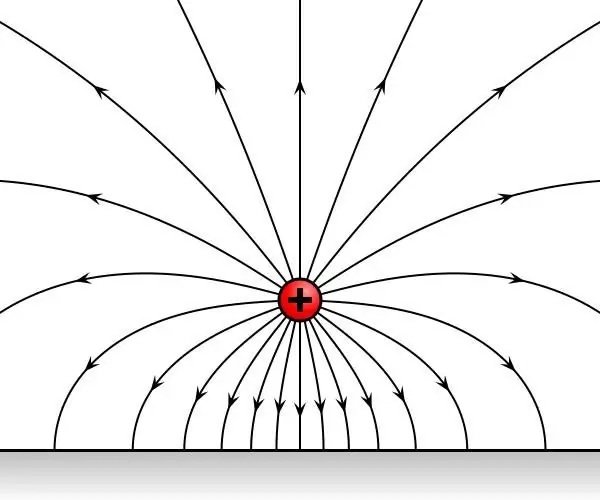
ในทางกลับกัน ลองพิจารณาประจุทดสอบสองอันที่นำมา วางต่อเนื่องที่จุดหนึ่งในอวกาศ ซึ่งอยู่ภายใต้อิทธิพลของสนามไฟฟ้าสถิต ปรากฎว่าค่าใช้จ่ายจะอยู่ภายใต้อิทธิพลที่ไม่เปลี่ยนแปลงตามเวลาในส่วนของเขา ให้ F₁ และ F_{2 เป็นกำลังในข้อกล่าวหา}

จากการสรุปข้อมูลการทดลอง พบว่ากองกำลัง F₁ และ F₂ ถูกกำหนดทิศทางอย่างใดอย่างหนึ่งหรือ ในทิศทางตรงกันข้ามและอัตราส่วน F₁/F₂ เป็นอิสระจากจุดในช่องว่างที่มีการเรียกเก็บเงินทดสอบสลับกัน ดังนั้นอัตราส่วน F₁/F_{2 จึงเป็นลักษณะพิเศษของตัวผู้เล่นเอง และไม่ขึ้นกับสนาม}

การค้นพบข้อเท็จจริงนี้ทำให้สามารถจำแนกลักษณะการใช้ไฟฟ้าของร่างกายได้ และต่อมาถูกเรียกว่าประจุไฟฟ้า ดังนั้นตามคำจำกัดความ q₁/q2_=F1_/F 2 _{โดยที่ q}1 _{และ q}2 _{- จำนวนเงินที่เรียกเก็บ ณ จุดหนึ่งของสนาม และ F 1} และ F₂ - กำลังดำเนินการโจมตีจากด้านข้างของสนาม

จากการพิจารณาดังกล่าว ขนาดของประจุของอนุภาคต่างๆ ได้ถูกทดลองสร้าง คุณสามารถคำนวณมูลค่าของประจุอื่นได้โดยการวัดอัตราส่วน F₁/F_2.

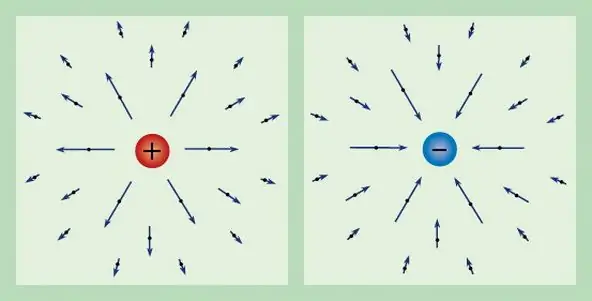
สนามไฟฟ้าใดๆ ก็สามารถจำแนกได้โดยใช้ประจุที่ทราบ ดังนั้น แรงที่กระทำต่อประจุทดสอบหนึ่งหน่วยที่อยู่นิ่งจึงเรียกว่าความแรงของสนามไฟฟ้าและเขียนแทนด้วย E จากคำจำกัดความของประจุ เราได้รับว่าเวกเตอร์ความแรงมีรูปแบบดังนี้ E=F/q.

การเชื่อมต่อของเวกเตอร์ j และ E. กฎของโอห์มอีกรูปแบบหนึ่ง

ในตัวนำที่เป็นเนื้อเดียวกัน การเคลื่อนที่ตามคำสั่งของอนุภาคที่มีประจุจะเกิดขึ้นในทิศทางของเวกเตอร์ E ซึ่งหมายความว่าเวกเตอร์ j และ E จะถูกกำกับร่วมกัน ในการกำหนดความหนาแน่นกระแส เราเลือกปริมาตรทรงกระบอกเล็ก ๆ ในตัวนำอย่างไม่สิ้นสุด จากนั้นกระแสไฟเท่ากับ jdS จะผ่านหน้าตัดของกระบอกสูบนี้ และแรงดันไฟฟ้าที่ใช้กับกระบอกสูบจะเท่ากับ Edl สูตรสำหรับความต้านทานของทรงกระบอกเป็นที่รู้จักกันเช่นกัน

จากนั้นเขียนสูตรสำหรับความแรงกระแสในสองวิธี เราได้ j=E/p โดยที่ค่า 1/p เรียกว่าค่าการนำไฟฟ้า และเป็นค่าผกผันของค่าความต้านทานไฟฟ้า โดยปกติจะแสดงเป็น σ (ซิกมา) หรือ λ (แลมบ์ดา) หน่วยของการนำไฟฟ้าคือ Sm/m โดยที่ Sm คือ Siemens หน่วยผกผันของโอห์ม

ดังนั้น เราสามารถตอบคำถามข้างต้นเกี่ยวกับกฎของโอห์มสำหรับวงจรที่ไม่เป็นเนื้อเดียวกันได้ ในกรณีนี้ พาหะปัจจุบันจะได้รับผลกระทบจากแรงจากสนามไฟฟ้าสถิต ซึ่งมีลักษณะเฉพาะโดยความเข้ม E₁ และแรงอื่นๆ ที่กระทำต่อพวกมันจากแหล่งกระแสอื่น ซึ่งสามารถ E ₂ ที่กำหนด แล้วกฎของโอห์มก็นำไปใช้กับส่วนที่ไม่เท่ากันของห่วงโซ่จะมีลักษณะดังนี้: j=λ(E₁ + E_2).

เพิ่มเติมเกี่ยวกับการนำไฟฟ้าและความต้านทาน

ความสามารถของตัวนำในการนำกระแสไฟฟ้ามีลักษณะเป็นความต้านทาน ซึ่งสามารถพบได้ผ่านสูตรความต้านทานหรือค่าการนำไฟฟ้าซึ่งคำนวณเป็นส่วนกลับของการนำไฟฟ้า ค่าของพารามิเตอร์เหล่านี้พิจารณาจากคุณสมบัติทางเคมีของวัสดุตัวนำและสภาวะภายนอก โดยเฉพาะอุณหภูมิแวดล้อม

สำหรับโลหะส่วนใหญ่ ความต้านทานที่อุณหภูมิปกติจะเป็นสัดส่วนกับมัน นั่นคือ p ~ T อย่างไรก็ตาม มีการสังเกตการเบี่ยงเบนที่อุณหภูมิต่ำ สำหรับโลหะและโลหะผสมจำนวนมากที่อุณหภูมิใกล้เคียงกับ 0°K การคำนวณความต้านทานจะแสดงค่าเป็นศูนย์ ปรากฏการณ์นี้เรียกว่าตัวนำยิ่งยวด ตัวอย่างเช่น ปรอท ดีบุก ตะกั่ว อะลูมิเนียม ฯลฯ มีคุณสมบัตินี้ โลหะแต่ละชนิดมีอุณหภูมิวิกฤตเป็นของตัวเอง T_{k ซึ่งสังเกตปรากฏการณ์ของความเป็นตัวนำยิ่งยวด}

โปรดทราบด้วยว่าคำจำกัดความของความต้านทานของทรงกระบอกสามารถสรุปให้ใช้กับสายไฟที่ทำจากวัสดุชนิดเดียวกันได้ ในกรณีนี้ พื้นที่หน้าตัดจากสูตรความต้านทานจะเท่ากับหน้าตัดของเส้นลวด และ l คือความยาว