พีระมิดร่วมกับปริซึมเป็นรูปทรงหลายเหลี่ยมที่สมบูรณ์แบบในพื้นที่สามมิติ ลักษณะทางเรขาคณิตของพวกมันได้รับการศึกษาในโรงเรียนมัธยมปลาย ในบทความนี้ เราจะพิจารณาว่าปิรามิดคืออะไร มีองค์ประกอบอะไรบ้าง และอธิบายลักษณะโดยย่อของปิรามิดที่ถูกต้องด้วย
ปิรามิดรูปเรขาคณิต
จากมุมมองของเรขาคณิต ปิรามิดเป็นรูปเชิงพื้นที่ซึ่งประกอบด้วยรูปหลายเหลี่ยมหนึ่งรูปและสามเหลี่ยมหลายรูป การหาตัวเลขนี้ค่อนข้างง่าย เมื่อต้องการทำสิ่งนี้ ให้นำรูปหลายเหลี่ยมที่มี n ด้าน จากนั้นเลือกจุดที่ต้องการในอวกาศซึ่งจะไม่อยู่ในระนาบของรูปหลายเหลี่ยม แล้วเชื่อมต่อจุดยอดของรูปหลายเหลี่ยมแต่ละจุดเข้ากับจุดนี้ เห็นได้ชัดว่า รูปที่เกิดขึ้นในลักษณะนี้จะมีรูปสามเหลี่ยม n รูปเชื่อมต่อกันที่จุดยอดเดียว
ถ่ายภาพรูปทรงเรขาคณิตของรูปที่อธิบายให้เห็นภาพ

รูปปิรามิดรูปสี่เหลี่ยม ฐานคือรูปสี่เหลี่ยม และพื้นผิวด้านข้างประกอบขึ้นจากสามเหลี่ยมสี่รูปที่มีจุดยอดร่วมกัน
องค์ประกอบพีระมิด
เช่นเดียวกับรูปทรงหลายเหลี่ยม ปิรามิดประกอบด้วยองค์ประกอบสามประเภท:
- ขอบ;
- tops;
- ซี่โครง
ใบหน้าเป็นส่วนหนึ่งของระนาบที่แยกปริมาตรภายในของร่างออกจากพื้นที่โดยรอบ ถ้าฐานของปิรามิดมี n-gon จำนวนของใบหน้าจะเป็น n+1 เสมอ ในจำนวนนี้ n ด้านเป็นรูปสามเหลี่ยม และด้านหนึ่งเป็นฐาน n-gonal ที่กล่าวถึง
จุดยอดคือจุดที่ใบหน้าของรูปตั้งแต่ 3 หน้าขึ้นไปตัดกัน บริเวณฐานประกอบด้วยจุดยอด n จุด ซึ่งแต่ละจุดประกอบด้วยใบหน้ารูปสามเหลี่ยมสองหน้าและฐานหนึ่งจุด จุดที่ด้านสามเหลี่ยมมาบรรจบกันเรียกว่ายอดปิรามิด ดังนั้น ตัวเลขที่กำลังพิจารณาประกอบด้วยจุดยอด n+1 จุด
ขอบเป็นเส้นตรงที่เกิดขึ้นเมื่อใบหน้าสองหน้าตัดกัน ขอบแต่ละด้านถูกล้อมรอบด้วยจุดยอดสองจุดที่ปลาย ปิรามิดใดๆ ที่มีฐาน n-gon จะมีขอบ 2n ครึ่งหนึ่งของจำนวนนี้คือ n เกิดขึ้นจากจุดตัดของสามเหลี่ยมด้านข้างเท่านั้น
ประเภทตัวเลขที่เป็นไปได้
ชื่อของรูปที่พิจารณาจะกำหนดโดยประเภทของรูปหลายเหลี่ยมที่ฐานโดยไม่ซ้ำกัน ตัวอย่างเช่น หากมีสามมุมและสามด้าน ปิรามิดจะเป็นรูปสามเหลี่ยม หากมีสี่ - สี่เหลี่ยม และอื่นๆ
รูปหลายเหลี่ยมสามารถนูนและเว้าได้เช่นเดียวกับแบบปกติและทั่วไป ทั้งหมดนี้ยังเป็นตัวกำหนดรูปลักษณ์ของปิรามิด
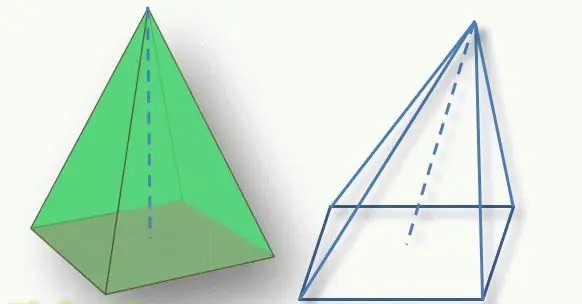
จุดสำคัญในการกำหนดประเภทของรูปคือตำแหน่งของยอดปิรามิดที่สัมพันธ์กับฐานของมัน ส่วนตั้งฉากที่ลากจากด้านบนถึงฐานรูปหลายเหลี่ยมเรียกว่าความสูงของรูป หากส่วนนี้ตัดกับฐานที่จุดศูนย์กลางทางเรขาคณิตของมัน (สำหรับรูปสามเหลี่ยม นี่คือจุดตัดของค่ามัธยฐาน สำหรับรูปสี่เหลี่ยมจัตุรัส จุดตัดของเส้นทแยงมุม) รูปทรงนั้นจะเรียกว่าเส้นตรง ไม่งั้นก็พูดถึงพีระมิดเอียง
ถ้า n-gon ของฐานเป็นปกติ (สามเหลี่ยมด้านเท่า สี่เหลี่ยมจัตุรัส ฯลฯ) และรูปเป็นเส้นตรง จะเรียกว่าปิรามิดปกติ
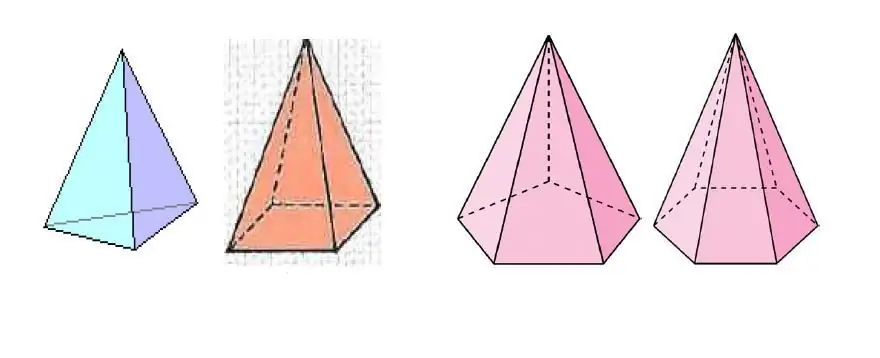
ภาพด้านบนแสดงปิรามิดหลายอัน ซึ่งมีจำนวนด้านของรูปหลายเหลี่ยมที่ฐานต่างกัน
คุณสมบัติของปิรามิดทั่วไป
ปิรามิดเหล่านี้แตกต่างจากร่างอื่นๆ ในกลุ่มนี้ด้วยความสมมาตรในระดับสูง ในแง่นี้ จะสะดวกต่อการคำนวณทางเรขาคณิตต่างๆ กับพวกมัน เช่น ปริมาตรหรือพื้นที่ผิว
ปิรามิดปกติมี n-gon อยู่ที่ฐาน ซึ่งพื้นที่นั้นถูกกำหนดอย่างเฉพาะตัวจากความรู้ด้านความยาวด้านของมัน พื้นผิวด้านข้างของรูปประกอบด้วยสามเหลี่ยมเหมือนกัน n รูป ซึ่งเป็นด้านเท่ากันหมด ขอบของปิรามิดปกติที่อยู่บนพื้นผิวด้านข้างนั้นเท่ากัน ค่าของความยาวของขอบนี้มักใช้ในการคำนวณหาเส้นตั้งฉากและกำหนดพื้นที่ผิว
ความสูงของปิรามิดธรรมดาเป็นลักษณะสำคัญที่สองของรูปร่าง (อันแรกคือความยาวของขอบเหตุ) ใช้ความสูงในการคำนวณปริมาตร
ระนาบใดๆ ขนานกับฐานซึ่งตัดกับด้านข้างของพีระมิด จะนำไปสู่การก่อตัวของส่วนรูปหลายเหลี่ยม เป็นโฮโมเทติกเมื่อเทียบกับรูปหลายเหลี่ยมฐาน การดำเนินการสไลซ์ที่อธิบายจะนำไปสู่การก่อตัวของตัวเลขใหม่ทั้งคลาส - ปิรามิดปกติที่ถูกตัดทอน
ปิรามิดที่มีชื่อเสียงที่สุด

แน่นอนว่านี่คือปิรามิดทรงสี่เหลี่ยมปกติของฟาโรห์อียิปต์ ในสถานที่ที่เรียกว่ากิซ่า มีอนุสาวรีย์หินมากกว่า 100 แห่ง ความสมบูรณ์แบบของการออกแบบและความแม่นยำของพารามิเตอร์ทางเรขาคณิตซึ่งทำให้นักวิทยาศาสตร์ประหลาดใจมาจนถึงทุกวันนี้ ที่ใหญ่ที่สุดคือ Pyramid of Cheops ซึ่งสูงประมาณ 146 เมตร และยาวประมาณ 230 เมตร
ปิรามิดเหล่านี้มีไว้ทำอะไร กลไกใดและสร้างขึ้นเมื่อใด ยังไม่มีใครรู้จนถึงทุกวันนี้

