ส่วนสำคัญของอุณหพลศาสตร์คือการศึกษาการเปลี่ยนแปลงระหว่างเฟสต่างๆ ของสาร เนื่องจากกระบวนการเหล่านี้เกิดขึ้นในทางปฏิบัติและมีความสำคัญพื้นฐานสำหรับการทำนายพฤติกรรมของระบบภายใต้เงื่อนไขบางประการ การเปลี่ยนแปลงเหล่านี้เรียกว่าการเปลี่ยนเฟส ซึ่งบทความนี้ใช้เฉพาะ
แนวคิดของเฟสและส่วนประกอบของระบบ

ก่อนที่จะพิจารณาการเปลี่ยนเฟสในฟิสิกส์ จำเป็นต้องกำหนดแนวคิดของเฟสเอง ดังที่ทราบจากวิชาฟิสิกส์ทั่วไป สสารมีสามสถานะ: ก๊าซ ของแข็ง และของเหลว ในส่วนพิเศษของวิทยาศาสตร์ - ในอุณหพลศาสตร์ - กฎหมายกำหนดขึ้นสำหรับเฟสของสสาร ไม่ใช่สำหรับสถานะของการรวมตัว เฟสเป็นที่เข้าใจกันว่าเป็นปริมาตรที่แน่นอนของสสารที่มีโครงสร้างเป็นเนื้อเดียวกัน มีลักษณะเฉพาะด้วยคุณสมบัติทางกายภาพและทางเคมีที่เฉพาะเจาะจง และแยกออกจากส่วนที่เหลือของสสารด้วยขอบเขต ซึ่งเรียกว่าเฟสอินเทอร์เฟส
ดังนั้น แนวคิดของ "เฟส" จึงมีข้อมูลที่สำคัญกว่ามากเกี่ยวกับคุณสมบัตินี้สสารมากกว่าสถานะของการรวมตัว ตัวอย่างเช่น สถานะของแข็งของโลหะ เช่น เหล็ก สามารถอยู่ในเฟสต่อไปนี้: ลูกบาศก์ที่มีศูนย์กลางอยู่ที่ตัวแม่เหล็กที่อุณหภูมิต่ำ (BCC) อุณหภูมิต่ำ bcc ที่ไม่ใช่แม่เหล็ก อุณหภูมิต่ำ ลูกบาศก์ที่อยู่กึ่งกลางใบหน้า (fcc) และสูง- bcc.อุณหภูมิที่ไม่ใช่แม่เหล็ก
นอกจากแนวคิดของ "เฟส" แล้ว กฎของเทอร์โมไดนามิกส์ยังใช้คำว่า "ส่วนประกอบ" ซึ่งหมายถึงจำนวนองค์ประกอบทางเคมีที่ประกอบเป็นระบบเฉพาะ ซึ่งหมายความว่าเฟสสามารถเป็นองค์ประกอบเดี่ยว (องค์ประกอบทางเคมี 1 รายการ) หรือหลายองค์ประกอบ (องค์ประกอบทางเคมีหลายรายการ)
ทฤษฎีบทของกิ๊บส์และสมดุลระหว่างเฟสของระบบ

เพื่อทำความเข้าใจการเปลี่ยนเฟส จำเป็นต้องรู้เงื่อนไขสมดุลระหว่างพวกเขา เงื่อนไขเหล่านี้หาได้ทางคณิตศาสตร์โดยการแก้ระบบสมการกิ๊บส์สำหรับสมการแต่ละสมการ โดยสมมติว่าถึงสภาวะสมดุลเมื่อพลังงานกิ๊บส์ทั้งหมดของระบบที่แยกได้จากอิทธิพลภายนอกไม่เปลี่ยนแปลง
จากการแก้ระบบสมการที่ระบุ จะได้เงื่อนไขสำหรับการดำรงอยู่ของดุลยภาพระหว่างหลายขั้นตอน: ระบบที่แยกออกมาจะยุติการพัฒนาต่อเมื่อความดัน ศักย์เคมีของแต่ละองค์ประกอบและอุณหภูมิในทุกเฟส มีค่าเท่ากัน
กิ๊บส์เฟสกฎเพื่อความสมดุล

ระบบที่ประกอบด้วยหลายเฟสและองค์ประกอบสามารถอยู่ในสมดุลได้ไม่เพียงเท่านั้นภายใต้เงื่อนไขบางประการ เช่น ที่อุณหภูมิและความดันจำเพาะ ตัวแปรบางตัวในทฤษฎีบท Gibbs สำหรับดุลยภาพสามารถเปลี่ยนแปลงได้ในขณะที่รักษาทั้งจำนวนเฟสและจำนวนส่วนประกอบที่อยู่ในสมดุลนี้ จำนวนตัวแปรที่สามารถเปลี่ยนแปลงได้โดยไม่รบกวนสมดุลในระบบเรียกว่าจำนวนอิสระของระบบนี้
จำนวนอิสระ l ของระบบที่ประกอบด้วยเฟส f และส่วนประกอบ k ถูกกำหนดจากกฎเฟสของกิ๊บส์อย่างไม่ซ้ำกัน กฎนี้เขียนทางคณิตศาสตร์ดังนี้ l + f=k + 2 จะทำงานกับกฎนี้อย่างไร ง่ายมาก. ตัวอย่างเช่น เป็นที่ทราบกันว่าระบบประกอบด้วยเฟสสมดุล f=3 จำนวนส่วนประกอบขั้นต่ำที่ระบบสามารถมีได้คือเท่าใด คุณสามารถตอบคำถามโดยให้เหตุผลดังต่อไปนี้: ในกรณีของสภาวะสมดุล เงื่อนไขที่เข้มงวดที่สุดจะเกิดขึ้นเมื่อมีการรับรู้ที่ตัวบ่งชี้บางตัวเท่านั้น นั่นคือ การเปลี่ยนแปลงในพารามิเตอร์ทางอุณหพลศาสตร์จะนำไปสู่ความไม่สมดุล ซึ่งหมายความว่าจำนวนอิสระ l=0 แทนที่ค่าที่รู้จักของ l และ f เราได้รับ k=1 นั่นคือระบบที่มีสามเฟสอยู่ในสมดุลสามารถประกอบด้วยองค์ประกอบเดียว ตัวอย่างที่สำคัญคือจุดสามจุดของน้ำ ซึ่งมีน้ำแข็ง น้ำของเหลว และไอน้ำอยู่ในสภาวะสมดุลที่อุณหภูมิและความดันจำเพาะ
การจำแนกประเภทของการแปลงเฟส
หากคุณเริ่มเปลี่ยนพารามิเตอร์ทางอุณหพลศาสตร์บางอย่างในระบบในสภาวะสมดุล คุณสามารถสังเกตได้ว่าเฟสหนึ่งจะหายไปและอีกเฟสหนึ่งจะปรากฏขึ้น ตัวอย่างง่ายๆ ของกระบวนการนี้คือน้ำแข็งละลายเมื่อถูกความร้อน
เนื่องจากสมการกิ๊บส์ขึ้นอยู่กับสองตัวแปรเท่านั้น (ความดันและอุณหภูมิ) และการเปลี่ยนเฟสเกี่ยวข้องกับการเปลี่ยนแปลงในตัวแปรเหล่านี้ จากนั้นในทางคณิตศาสตร์การเปลี่ยนแปลงระหว่างเฟสสามารถอธิบายได้โดยการแยกความแตกต่างของพลังงานกิ๊บส์ด้วยความเคารพ ตัวแปร วิธีนี้เป็นวิธีที่ Paul Ehrenfest นักฟิสิกส์ชาวออสเตรียใช้ในปี 1933 เมื่อเขารวบรวมการจัดหมวดหมู่ของกระบวนการทางอุณหพลศาสตร์ที่รู้จักทั้งหมดซึ่งเกิดขึ้นพร้อมกับการเปลี่ยนแปลงในสมดุลของเฟส
จากพื้นฐานของเทอร์โมไดนามิกส์ อนุพันธ์อันดับแรกของพลังงานกิ๊บส์เทียบกับอุณหภูมิเท่ากับการเปลี่ยนแปลงในเอนโทรปีของระบบ อนุพันธ์ของพลังงานกิ๊บส์เทียบกับความดันเท่ากับการเปลี่ยนแปลงของปริมาตร หากเฟสในระบบเปลี่ยนไป เอนโทรปีหรือโวลุ่มหยุดนิ่ง นั่นคือ การเปลี่ยนแปลงอย่างกะทันหัน แสดงว่ามีการเปลี่ยนเฟสลำดับแรก
นอกจากนี้ อนุพันธ์อันดับสองของพลังงานกิ๊บส์เทียบกับอุณหภูมิและความดันคือความจุความร้อนและค่าสัมประสิทธิ์การขยายตัวเชิงปริมาตรตามลำดับ หากการเปลี่ยนแปลงระหว่างเฟสมีความไม่ต่อเนื่องในค่าของปริมาณทางกายภาพที่ระบุ เราจะพูดถึงการเปลี่ยนเฟสลำดับที่สอง
ตัวอย่างการแปลงระหว่างเฟส

มีลักษณะทรานสิชั่นที่แตกต่างกันมากมาย ภายในกรอบของการจำแนกประเภทนี้ ตัวอย่างที่โดดเด่นของการเปลี่ยนประเภทแรกคือกระบวนการหลอมโลหะหรือการควบแน่นของไอน้ำจากอากาศ เมื่อมีปริมาตรเพิ่มขึ้นในระบบ
ถ้าเราพูดถึงการเปลี่ยนลำดับที่สอง ตัวอย่างที่โดดเด่นคือการเปลี่ยนแปลงของเหล็กจากสถานะแม่เหล็กเป็นสถานะพาราแมกเนติกที่อุณหภูมิ768 ºC หรือการแปรสภาพของตัวนำโลหะให้อยู่ในสถานะตัวนำยิ่งยวดที่อุณหภูมิใกล้กับศูนย์สัมบูรณ์
สมการที่อธิบายการเปลี่ยนประเภทแรก
ในทางปฏิบัติ บ่อยครั้งจำเป็นต้องรู้ว่าการเปลี่ยนแปลงของอุณหภูมิ ความดัน และพลังงานดูดซับ (ที่ปล่อยออกมา) ในระบบเมื่อการเปลี่ยนแปลงเฟสเกิดขึ้นในนั้น ใช้สมการสำคัญสองสมการเพื่อจุดประสงค์นี้ ได้มาจากความรู้พื้นฐานของอุณหพลศาสตร์:
- สูตรของคลาเปยรอนซึ่งกำหนดความสัมพันธ์ระหว่างความดันและอุณหภูมิระหว่างการเปลี่ยนแปลงระหว่างเฟสต่างๆ
- Clausius สูตรที่เชื่อมโยงพลังงานที่ถูกดูดซับ (ปล่อยออกมา) กับอุณหภูมิของระบบในระหว่างการแปลง
การใช้สมการทั้งสองนี้ไม่เพียงแต่จะได้การพึ่งพาเชิงปริมาณของปริมาณทางกายภาพเท่านั้น แต่ยังรวมถึงการกำหนดสัญญาณของความชันของเส้นโค้งสมดุลบนแผนภาพเฟสด้วย
สมการอธิบายการเปลี่ยนประเภทที่สอง

การเปลี่ยนเฟสของประเภทที่ 1 และ 2 อธิบายด้วยสมการที่ต่างกัน เนื่องจากการใช้สมการคลอเซียสและคลอลิอุสสำหรับการเปลี่ยนลำดับที่สองทำให้เกิดความไม่แน่นอนทางคณิตศาสตร์
เพื่ออธิบายอย่างหลัง จะใช้สมการ Ehrenfest ซึ่งสร้างความสัมพันธ์ระหว่างการเปลี่ยนแปลงของความดันและอุณหภูมิผ่านความรู้เกี่ยวกับการเปลี่ยนแปลงความจุความร้อนและสัมประสิทธิ์การขยายตัวเชิงปริมาตรระหว่างกระบวนการเปลี่ยนรูป สมการเอเรนเฟสต์ใช้เพื่ออธิบายการเปลี่ยนผ่านของตัวนำ-ตัวนำยิ่งยวดในกรณีที่ไม่มีสนามแม่เหล็ก
ความสำคัญไดอะแกรมเฟส
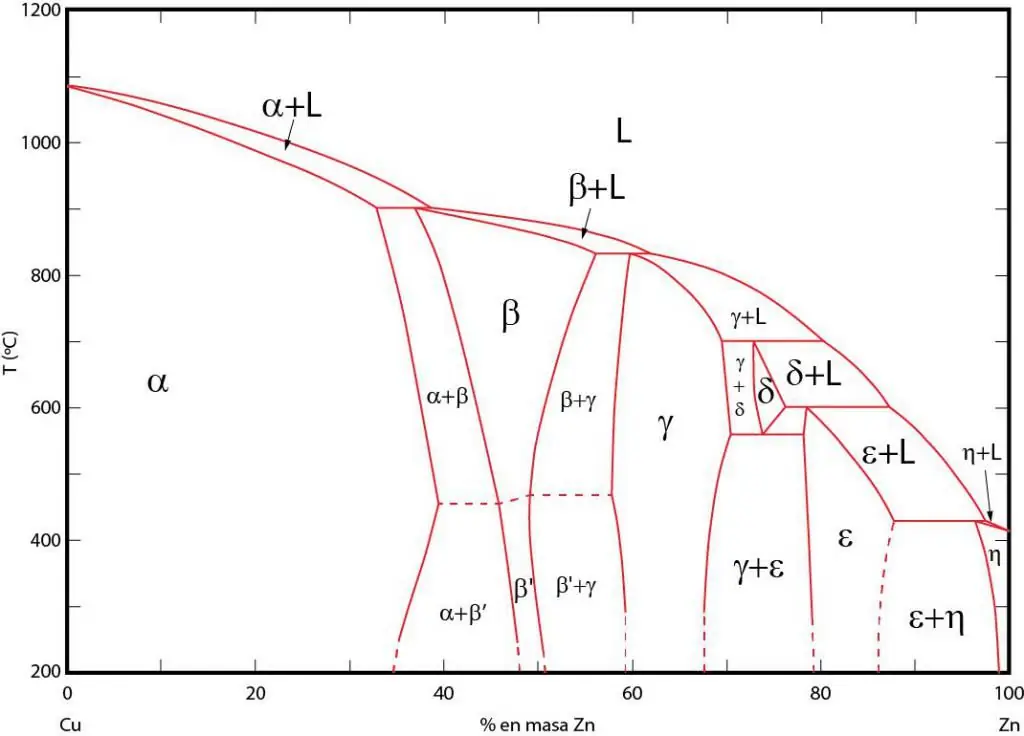
แผนภาพเฟสคือการแสดงภาพกราฟิกของพื้นที่ที่มีเฟสที่สอดคล้องกันอยู่ในสมดุล พื้นที่เหล่านี้คั่นด้วยเส้นสมดุลระหว่างเฟส แผนภาพเฟส P-T (ความดัน-อุณหภูมิ), T-V (อุณหภูมิ-ปริมาตร) และ P-V (ปริมาตรความดัน) มักใช้
ความสำคัญของไดอะแกรมเฟสอยู่ที่ความจริงที่ว่ามันช่วยให้คุณคาดการณ์ได้ว่าระบบจะอยู่ในระยะใดเมื่อสภาวะภายนอกเปลี่ยนแปลงไปตามนั้น ข้อมูลนี้ใช้ในการรักษาความร้อนของวัสดุต่างๆ เพื่อให้ได้โครงสร้างที่มีคุณสมบัติตามที่ต้องการ

