เพื่อที่จะสามารถวาดภาพบนวัตถุกระดาษที่ในความเป็นจริงไม่มีขนาดที่ "สะดวก" มาก ผู้คนจึงสร้างมาตราส่วนขึ้นมา อันที่จริง สิ่งนี้อธิบายว่ามาตราส่วนมีไว้เพื่ออะไร
เมื่อหลักสูตรโรงเรียนเริ่มเปิดเผยแนวคิดเรื่องขนาด
เป็นครั้งแรกที่เด็กๆ จะเจอคำนี้ขณะศึกษาแผนที่และแผนผังของพื้นที่ ครูอธิบายว่าเหตุใดจึงต้องใช้มาตราส่วน แสดงอะไร โดยใช้ Atlases เป็นตัวอย่าง มีการอธิบายว่าสถานที่ทางภูมิศาสตร์ใดๆ มีขนาดใหญ่มากจนเป็นการยากและไม่สะดวกที่จะพรรณนาในขนาดเต็ม
ผู้คนดึงภูมิประเทศในรูปแบบที่เล็กลง แต่สำหรับสิ่งนี้พวกเขาไม่ได้ใช้อัตราส่วนที่แน่นอน ตอนนี้กำลังดำเนินการอย่างชาญฉลาดยิ่งขึ้น - แต่ละเส้นประและเส้นที่แสดงบนแผนที่มีขนาดที่สามารถคูณด้วยจำนวนหนึ่งและค้นหาความยาวและความกว้างที่แท้จริง
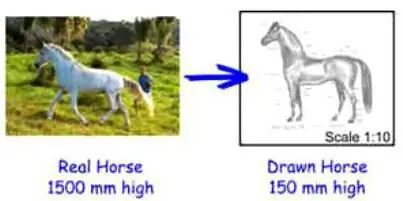
บันทึกขนาด: วิธีแรกในการอ่าน
มาตราส่วนถูกระบุด้วยตัวเลขสองตัวคั่นด้วยเครื่องหมายทวิภาค หลักแรกระบุหน่วยของมิติในรูปที่สองระบุจำนวนหน่วยจริงในรูปที่ตรงกับตัวเลขแรก ตัวอย่างเช่น หากบางแผนระบุมาตราส่วน 1:1000 และหน่วยของขนาดระบุเป็นเซนติเมตร ดังนั้นหนึ่งเซนติเมตรในรูปจะเท่ากับ 1,000 ซม. ในความเป็นจริง แล้วมาตราส่วนมีไว้เพื่ออะไร? ด้วยความช่วยเหลือนี้ คุณไม่เพียงแต่สามารถลดวัตถุบางอย่างในแผนกราฟิกได้เท่านั้น แต่ยังคำนวณขนาดจริงของวัตถุเหล่านั้นได้อย่างแม่นยำด้วย
วิธีที่สองในการบันทึกมาตราส่วน: สะดวกอะไร
วิธีการก่อนหน้าในการเขียนมาตราส่วนผ่านทวิภาคเรียกว่าตัวเลข แต่ยังมีมาตราส่วนชื่อ บันทึกของเขามีดังนี้: 1 ซม. - 20 กม. ปรากฎว่าด้วยวิธีนี้ เป็นไปได้ที่จะเขียนมาตราส่วนขนาดใหญ่ที่จะไม่แสดงด้วยตัวเลขที่มีศูนย์หลายตัวหากสถานการณ์เกิดขึ้นเมื่อจำเป็นต้องระบุหลายร้อยกิโลเมตรในหนึ่งเซนติเมตร ในขณะเดียวกันก็ชัดเจนทันทีว่าเท่าไหร่อะไรและอะไร บันทึกนี้ใช้งานง่ายและชัดเจนยิ่งขึ้น
การปรับขนาดในภาพวาด: สิ่งที่ช่วยเสริมแนวคิดที่ศึกษาก่อนหน้านี้
แนวคิดเรื่องขนาดไม่เพียงแต่พบในภูมิศาสตร์เท่านั้น แต่ยังพบในการศึกษาเรื่องเช่นการวาดภาพด้วย ใช้หลักการเดียวกันนี้เพื่อพรรณนาวัตถุต่างๆ แต่มีข้อแตกต่างที่สำคัญ: ในที่นี้ แนวคิดเกี่ยวกับมาตราส่วนสำหรับขนาดใดก็ขยายออกไปด้วยข้อเท็จจริงที่ว่ามันสามารถใช้เพื่อพรรณนารายละเอียดเล็กๆ น้อยๆ ในระดับที่ใหญ่ขึ้นได้ ในภูมิศาสตร์เราไม่ได้พูดถึงเรื่องนี้เพราะไม่มีวัตถุขนาดเล็กในภูมิศาสตร์ที่จำเป็นต้องขยายให้ใหญ่ขึ้น ทวีป ภูเขา แม่น้ำ และทะเลสาบ มีขนาดใหญ่กว่ากระดาษ A4 หรือแม้แต่A1.
กำลังศึกษาภาพวาด คุณสามารถใช้สเกลเพื่อวาดรายละเอียดที่เล็กที่สุดในรูปแบบที่ใหญ่ขึ้น เช่น สลักเกลียวหรือฟันเฟือง
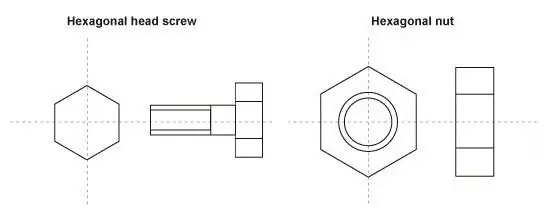
แล้วทำไมเราต้องมีมาตราส่วนในกรณีนี้? ด้วยความช่วยเหลือ คุณสามารถวาดภาพองค์ประกอบขนาดเล็กได้อย่างสะดวก ชัดเจน และละเอียดยิ่งขึ้น ในกรณีนี้ การกลับกันเกิดขึ้นในสัญกรณ์: ตัวเลขแรกจะมากกว่าวินาที และสัญกรณ์ 100:1 จะฟังดังนี้: 100 หน่วยเมตริกของรูปภาพสอดคล้องกับหนึ่งหน่วยของขนาดจริง
บางตัวอย่างที่ชัดเจน
มาตราส่วนคืออะไร ในกรณีของรูปภาพของวัตถุขนาดเล็ก มันแสดงอะไร ผลลัพธ์บนกระดาษคืออะไร อีกครั้ง เรามีอัตราส่วนที่แน่นอนของขนาดของรูปภาพของชิ้นส่วนและวัตถุจริง เรียกคืนมาตราส่วน 100: 1 เดียวกัน ปรากฎว่าในรูปหนึ่งร้อยมิลลิเมตรมีขนาดจริงเพียงหนึ่งมิลลิเมตร หากส่วนใดส่วนหนึ่งในภาพกว้าง 500 มม. ความกว้างจริงเพียง 5 มม.
ถ้าเราจำกรณีแรกได้ รูปภาพบนแผ่นงานสำเนาขนาดเล็กของวัตถุขนาดใหญ่ มาตราส่วน 1:100 จะหมายความว่าหนึ่งมิลลิเมตรในภาพจะมีขนาดจริง 100 มม. ดังนั้น หากวัตถุมีความยาว 80 มม. บนภาพวาดหรือแผนที่ ความยาวจริงของวัตถุจะเท่ากับ 8000 มม. ตัวอย่างที่ชัดเจนว่าขนาดมีไว้เพื่ออะไรและเป็นสิ่งประดิษฐ์ที่สะดวกสบายของมนุษยชาติอย่างไร
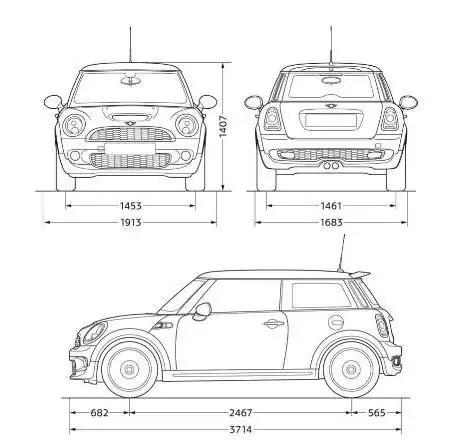
การใช้ตาชั่งสำคัญทันทีโปรดจำไว้ว่าตัวเลขแรกหมายถึงภาพและตัวเลขที่สองหมายถึงขนาดที่แท้จริงของวัตถุ เพื่อไม่ให้สับสนในอนาคต เพื่อรวบรวมรากฐานเหล่านี้ ชั้นเรียนภาคปฏิบัติในวิชาภูมิศาสตร์จะจัดขึ้นในโรงเรียนเพื่อให้เด็ก ๆ อธิบายและคำนวณขนาดของวัตถุจริงหลายครั้งโดยใช้แผนที่ สิ่งเดียวกันเกิดขึ้นในบทเรียนการวาดภาพ
สรุป
มาตราส่วนมีไว้เพื่ออะไร? คำตอบสำหรับคำถามนี้ประกอบด้วยสามประเด็นที่คุณต้องจำไว้:
- อย่างแรก - ต้องใช้มาตราส่วนเพื่อแสดงวัตถุขนาดใหญ่บนพื้นผิวที่สะดวกต่อการดู
- วินาที - ต้องใช้มาตราส่วนเพื่อแสดงภาพวัตถุขนาดเล็กในขนาดที่ใหญ่ขึ้น
- สาม - จำเป็นต้องใช้มาตราส่วนเพื่อให้สามารถกำหนดขนาดของวัตถุจริงได้อย่างแม่นยำ โดยไม่คำนึงถึงขนาดเริ่มต้น เล็กหรือใหญ่

