เมื่อเรียนฟิสิกส์ ป.10 พิจารณาหัวข้อไดโพล แนวคิดนี้หมายความว่าอย่างไรและใช้สูตรใดในการคำนวณ
แนะนำตัว
หากคุณวางไดโพลในช่องว่างของสนามไฟฟ้าที่สม่ำเสมอ คุณสามารถแสดงมันเป็นเส้นแรงได้ ไดโพลเป็นระบบที่มีประจุสองประจุที่เหมือนกันในพารามิเตอร์ แต่มีประจุตรงข้ามกัน ยิ่งไปกว่านั้น ระยะห่างระหว่างจุดทั้งสองจะน้อยกว่าระยะทางถึงจุดใดๆ ของสนามไดโพลมาก แนวคิดของโมเมนต์ไดโพลได้รับการศึกษาในหลักสูตรอิเล็กโทรไดนามิกของโรงเรียน (เกรด 10)
แกนไดโพลเป็นเส้นตรงที่ผ่านจุดของประจุทั้งสอง แขนไดโพลเป็นเวกเตอร์ที่เชื่อมต่อประจุและในขณะเดียวกันก็เปลี่ยนจากอนุภาคที่มีประจุลบไปเป็นอนุภาคที่มีประจุบวก ไดโพลไฟฟ้ามีลักษณะของการมีอยู่ของสถานะเช่นไดโพลหรือโมเมนต์ไฟฟ้า
ตามคำจำกัดความ โมเมนต์ไดโพลคือเวกเตอร์ที่เท่ากับผลคูณของประจุไดโพลและแขนของโมเมนต์ นอกจากนี้ยังกำกับร่วมกับไหล่ของไดโพล ที่ศูนย์เท่ากันของผลรวมของแรง เราคำนวณค่าของโมเมนต์ สำหรับมุมที่มีอยู่ระหว่างโมเมนต์ไดโพลกับทิศทางของสนามไฟฟ้า การปรากฏตัวของโมเมนต์เชิงกลเป็นลักษณะเฉพาะ
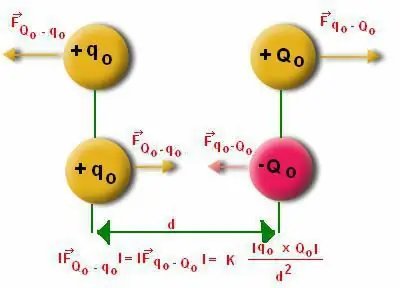
บ่อยครั้งที่ผู้คนพบว่าการคำนวณโมดูลัสที่กระทำต่อโครงสร้างไดโพลเป็นเรื่องยาก ที่นี่จำเป็นต้องคำนึงถึงลักษณะเฉพาะของการคำนวณมุม "อัลฟ่า" เป็นที่ทราบกันว่าไดโพลเบี่ยงเบนจากตำแหน่งที่สมดุล แต่โมเมนต์ไดโพลนั้นมีลักษณะการฟื้นตัว เนื่องจากมันมีแนวโน้มที่จะเคลื่อนไหว
การคำนวณ
เมื่อโมเมนต์ไดโพลนี้วางอยู่ในตัวกลางของสนามไฟฟ้าที่ไม่เป็นเนื้อเดียวกัน แรงจะเกิดขึ้นอย่างหลีกเลี่ยงไม่ได้ ในสภาพแวดล้อมเช่นนี้ ตัวชี้วัดผลรวมของแรงจะไม่เป็นศูนย์ ดังนั้นจึงมีแรงที่กระทำต่อโมเมนต์ไดโพลด้วยอักขระแบบจุด ขนาดของแขนไดโพลเล็กกว่ามาก
สูตรสามารถเขียนได้ดังนี้: F=q (E2 - E1)=qdE โดยที่ d คือส่วนต่างสนามไฟฟ้า
ค้นหาลักษณะของแนวคิดทางกายภาพภายใต้การศึกษา
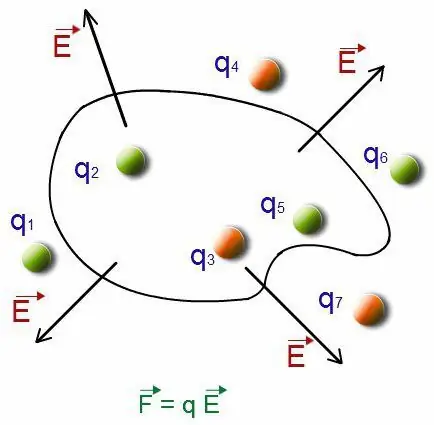
มาดูหัวข้อกันต่อครับ เพื่อกำหนดลักษณะเฉพาะของสนามไฟฟ้า ถ้ามันถูกสร้างขึ้นโดยใช้ระบบประจุและแปลเป็นภาษาท้องถิ่นในพื้นที่ขนาดเล็ก จำเป็นต้องทำการคำนวณจำนวนหนึ่ง ตัวอย่างนำเสนอโดยอะตอมและโมเลกุล ซึ่งในองค์ประกอบของพวกมันมีนิวเคลียสและอิเล็กตรอนที่มีประจุไฟฟ้า
หากจำเป็นต้องค้นหาฟิลด์ที่ระยะห่างมากกว่ามิติที่ประกอบเป็นพื้นที่ที่มีอนุภาค เราจะใช้สูตรที่แน่นอนจำนวนหนึ่งที่มีความซับซ้อนสูง เป็นไปได้ที่จะใช้ง่ายกว่านิพจน์โดยประมาณ สมมติว่าชุดประจุ qk มีส่วนร่วมในการสร้างสนามไฟฟ้า พวกเขาตั้งอยู่ในพื้นที่ขนาดเล็ก
ในการคำนวณคุณสมบัติที่มี อนุญาตให้รวมค่าธรรมเนียมทั้งหมดของระบบ ระบบดังกล่าวถือเป็นจุดชาร์จ Q ตัวบ่งชี้ขนาดจะเป็นผลรวมของประจุที่อยู่ในระบบเดิม
สถานที่เก็บค่าบริการ
ลองนึกภาพว่าตำแหน่งของการเรียกเก็บเงินถูกระบุไว้ในที่ใดก็ตามที่มีระบบการเรียกเก็บเงิน qk ตั้งอยู่ เมื่อทำการเปลี่ยนแปลงสถานที่ หากมีข้อ จำกัด ที่แสดงในพื้นที่เล็ก ๆ อิทธิพลดังกล่าวจะเล็กน้อยและแทบจะมองไม่เห็นในสนามเมื่อมอง ภายในขอบเขตของการประมาณความแรงและศักยภาพที่สนามไฟฟ้ามี การคำนวณจะทำโดยใช้สูตรดั้งเดิม
เมื่อผลรวมของประจุทั้งหมดของระบบเป็นศูนย์ พารามิเตอร์ของการประมาณที่ระบุจะดูหยาบ นี่เป็นเหตุผลที่สรุปได้ว่าไม่มีสนามไฟฟ้า หากจำเป็นต้องได้ค่าประมาณที่แม่นยำยิ่งขึ้น ให้รวบรวมกลุ่มของประจุบวกและประจุลบของระบบที่อยู่ระหว่างการพิจารณาแยกกัน
ในกรณีของการกระจัดของ "ศูนย์กลาง" ที่สัมพันธ์กับพารามิเตอร์อื่นๆ พารามิเตอร์ของฟิลด์ในระบบดังกล่าวสามารถอธิบายได้ว่าเป็นฟิลด์ที่มีประจุสองจุดซึ่งมีขนาดเท่ากันและอยู่ตรงข้ามในเครื่องหมาย มีข้อสังเกตว่าพวกเขาพลัดถิ่นเมื่อเทียบกับผู้อื่น เพื่อให้เพื่อการกำหนดลักษณะเฉพาะของระบบประจุในแง่ของพารามิเตอร์ของการประมาณนี้ จำเป็นต้องศึกษาคุณสมบัติของไดโพลในสนามไฟฟ้า
บทนำ
กลับคำนิยามกัน ไดโพลไฟฟ้าคือนิยามของระบบที่มีประจุสองจุด พวกมันมีขนาดเท่ากันและมีเครื่องหมายตรงข้ามกัน นอกจากนี้ ป้ายดังกล่าวยังอยู่ห่างจากป้ายอื่นๆ เพียงเล็กน้อย
คุณสามารถคำนวณคุณลักษณะของกระบวนการที่สร้างขึ้นโดยใช้ไดโพล และแสดงด้วยประจุสองจุด: +q และ −q และพวกมันอยู่ในระยะห่างที่สัมพันธ์กับประจุอื่นๆ

ลำดับการคำนวณ
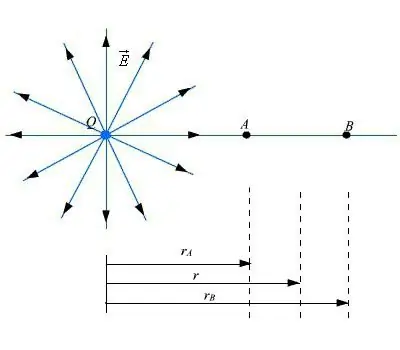
เริ่มด้วยการคำนวณศักยภาพและความเข้มที่ไดโพลมีบนพื้นผิวแกน นี่คือเส้นตรงที่วิ่งระหว่างประจุสองประจุ โดยมีเงื่อนไขว่าจุด A อยู่ที่ระยะห่างเท่ากับ r สัมพันธ์กับส่วนกลางของไดโพล และหากเป็น r >> a ตามหลักการทับซ้อนของศักย์สนาม ณ จุดนี้ ก็จะให้เหตุผลว่า ใช้นิพจน์เพื่อคำนวณพารามิเตอร์ของไดโพลไฟฟ้า
ขนาดเวกเตอร์กำลังคำนวณโดยหลักการซ้อนทับในการคำนวณความแรงของสนาม แนวคิดของอัตราส่วนของศักยภาพและความแรงของสนามจะใช้:
Ex=−Δφ /Δx.
ภายใต้เงื่อนไขดังกล่าว ทิศทางของเวกเตอร์ความเข้มจะถูกระบุตามยาวสัมพันธ์กับแกนไดโพล ในการคำนวณโมดูลัส ใช้สูตรมาตรฐาน
สำคัญคำชี้แจง
ควรคำนึงว่าสนามไดโพลไฟฟ้าอ่อนตัวเร็วกว่าที่เกิดการชาร์จแบบจุด การสลายตัวของศักย์สนามไดโพลจะแปรผกผันกับกำลังสองของระยะทาง และความแรงของสนามจะแปรผกผันกับลูกบาศก์ของระยะทาง
โดยใช้วิธีการที่คล้ายกันแต่ยุ่งยากกว่านั้น พารามิเตอร์ของศักย์ไฟฟ้าและความแรงของสนามของไดโพลจะพบที่จุดใดๆ พารามิเตอร์ตำแหน่งจะถูกกำหนดโดยใช้วิธีการคำนวณเช่น พิกัดเชิงขั้ว: ระยะทางถึง ศูนย์กลางของไดโพลไฟฟ้า (r) และมุม (θ).
การคำนวณโดยใช้เวกเตอร์ความตึง
แนวคิดของเวกเตอร์ความเข้ม E แบ่งออกเป็นสองจุด:
- รัศมี (Er) ซึ่งชี้ไปในทิศทางตามยาวสัมพันธ์กับเส้นตรง
- เส้นตรงดังกล่าวเชื่อมจุดที่กำหนดกับจุดศูนย์กลางของไดโพลกับเส้นตั้งฉากกับมัน Eθ.
การสลายตัวของแต่ละองค์ประกอบนี้นำไปสู่การเปลี่ยนแปลงที่เกิดขึ้นพร้อมกับพิกัดทั้งหมดของจุดที่จะสังเกต คุณสามารถหาได้จากอัตราส่วนที่เกี่ยวข้องกับตัวบ่งชี้ความแรงของสนามกับการปรับเปลี่ยนที่อาจเกิดขึ้น
การหาองค์ประกอบเวกเตอร์ที่ความแรงของสนาม สิ่งสำคัญคือต้องสร้างธรรมชาติของความสัมพันธ์ในการเปลี่ยนแปลงที่อาจเกิดขึ้นเนื่องจากการกระจัดของจุดสังเกตไปในทิศทางของเวกเตอร์
คำนวณองค์ประกอบตั้งฉาก
เมื่อเสร็จแล้วสำหรับขั้นตอนนี้ สิ่งสำคัญที่ต้องคำนึงว่านิพจน์สำหรับขนาดที่การกระจัดในแนวตั้งฉากขนาดเล็กจะถูกกำหนดโดยการเปลี่ยนมุม: Δl=rΔθพารามิเตอร์ขนาดสำหรับองค์ประกอบฟิลด์นี้จะเท่ากัน
เมื่อได้อัตราส่วนแล้ว ก็เป็นไปได้ที่จะกำหนดสนามของไดโพลไฟฟ้าที่จุดใดก็ได้เพื่อสร้างภาพด้วยเส้นแรงของสนามนี้
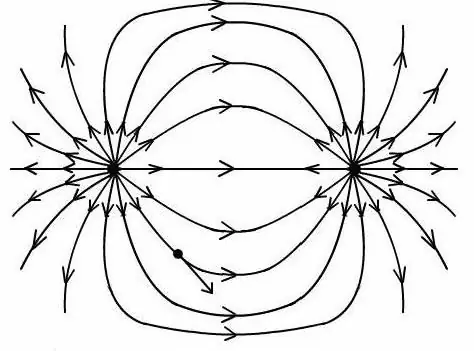
เป็นสิ่งสำคัญที่จะต้องพิจารณาว่าสูตรทั้งหมดสำหรับกำหนดศักยภาพและความแรงของสนามของไดโพลจะทำงานเฉพาะกับผลคูณของค่าที่มีประจุไดโพลหนึ่งประจุและระยะห่างระหว่างพวกมัน
โมเมนต์ไดโพล
ชื่องานอธิบายเป็นคำอธิบายแบบสมบูรณ์ของประเภทคุณสมบัติทางไฟฟ้า มีชื่อ "ไดโพลโมเมนต์ของระบบ"
ตามคำจำกัดความของไดโพลซึ่งเป็นระบบของประจุแบบจุด จะพบว่ามีลักษณะสมมาตรตามแกน เมื่อแกนเป็นเส้นตรงที่ผ่านประจุหลายประจุ
หากต้องการกำหนดคุณลักษณะทั้งหมดของไดโพล ให้ระบุทิศทางการวางแนวที่แกนมี เพื่อความง่ายในการคำนวณ สามารถระบุเวกเตอร์โมเมนต์ไดโพลได้ ค่าของขนาดของมันเท่ากับขนาดของโมเมนต์ไดโพล และเวกเตอร์ทิศทางต่างกันไปตามความบังเอิญของมันกับแกนของไดโพล ดังนั้น p=qa ถ้า a คือทิศทางของเวกเตอร์ที่เชื่อมประจุลบและประจุบวกของไดโพล
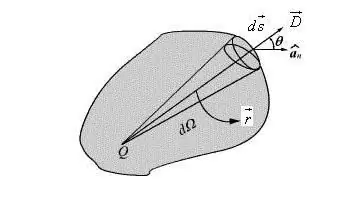
การใช้ลักษณะเฉพาะของไดโพลดังกล่าวสะดวกและทำให้ในกรณีส่วนใหญ่ทำให้สูตรง่ายขึ้นและให้รูปแบบเวกเตอร์ คำอธิบายของศักยภาพของสนามไดโพล ณ จุดทิศทางใดก็ได้เขียนในรูปของเวกเตอร์
การนำแนวคิดดังกล่าวเป็นคุณลักษณะเวกเตอร์ของไดโพลและโมเมนต์ไดโพลของมันสามารถดำเนินการได้โดยใช้แบบจำลองแบบง่าย − ประจุแบบจุดในสนามสม่ำเสมอ ซึ่งรวมถึงระบบของประจุ ซึ่งมิติทางเรขาคณิตนั้นทำ ไม่จำเป็นต้องนำมาพิจารณา แต่สิ่งสำคัญคือต้องทราบโมเมนต์ไดโพล นี่เป็นข้อกำหนดเบื้องต้นสำหรับการคำนวณ
พฤติกรรมของไดโพล
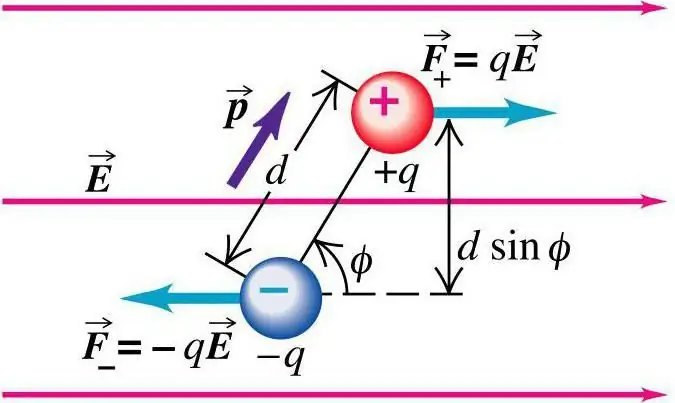
พฤติกรรมของไดโพลสามารถเห็นได้จากตัวอย่างสถานการณ์ดังกล่าว ตำแหน่งของประจุสองจุดมีลักษณะของระยะทางที่แน่นอนซึ่งสัมพันธ์กัน พวกเขาถูกวางไว้ในเงื่อนไขของไดโพลของสนามไฟฟ้าสม่ำเสมอ ได้สังเกตกระบวนการ ในบทเรียนฟิสิกส์ (อิเล็กโทรไดนามิกส์) แนวคิดนี้ได้รับการพิจารณาอย่างละเอียด จากสนามสู่การจู่โจม การกระทำของกองกำลังจะดำเนินการ:
F=±qE
มีขนาดเท่ากันและมีทิศทางตรงกันข้าม ตัวบ่งชี้ของแรงทั้งหมดที่กระทำบนไดโพลเป็นศูนย์ เนื่องจากแรงดังกล่าวส่งผลต่อจุดต่างๆ ช่วงเวลารวมจะเป็น:
M=ฟ้าบาป a=qEa บาป a=pE บาป a
โดยที่ α เป็นมุมที่เชื่อมเวกเตอร์ความแรงของสนามกับเวกเตอร์โมเมนต์ไดโพล เนื่องจากการมีอยู่ของโมเมนต์แรง โมเมนต์ไดโพลของระบบจึงมีแนวโน้มที่จะกลับไปยังทิศทางของเวกเตอร์ความแรงของสนามไฟฟ้า
ไดโพลไฟฟ้าเป็นแนวคิดที่สำคัญที่ต้องทำความเข้าใจให้ชัดเจน คุณสามารถอ่านเพิ่มเติมเกี่ยวกับเรื่องนี้ได้ทางอินเทอร์เน็ต นอกจากนี้ยังสามารถไปเรียนวิชาฟิสิกส์ที่โรงเรียนตอนป.10 ตามที่คุยกันด้านบน






