การศึกษากระบวนการที่เกิดขึ้นในระบบสถิตินั้นซับซ้อนด้วยขนาดอนุภาคขั้นต่ำและจำนวนมหาศาล แทบจะเป็นไปไม่ได้เลยที่จะพิจารณาแต่ละอนุภาคแยกกัน ดังนั้นจึงแนะนำปริมาณทางสถิติ: ความเร็วเฉลี่ยของอนุภาค ความเข้มข้นของอนุภาค มวลอนุภาค สูตรที่กำหนดลักษณะเฉพาะของระบบโดยคำนึงถึงพารามิเตอร์ด้วยกล้องจุลทรรศน์เรียกว่าสมการพื้นฐานของทฤษฎีโมเลกุล-จลนศาสตร์ของก๊าซ (MKT)
เล็กน้อยเกี่ยวกับความเร็วของอนุภาคเฉลี่ย
การทดลองหาความเร็วของอนุภาคได้ดำเนินการในขั้นแรก การทดลองที่รู้จักกันดีจากหลักสูตรของโรงเรียนซึ่งดำเนินการโดย Otto Stern ทำให้สามารถสร้างแนวคิดเกี่ยวกับความเร็วของอนุภาคได้ ในระหว่างการทดลอง ได้ทำการศึกษาการเคลื่อนที่ของอะตอมเงินในกระบอกสูบที่หมุนได้: ขั้นแรกให้อยู่ในสถานะคงที่ของการติดตั้ง จากนั้นเมื่อมันหมุนด้วยความเร็วเชิงมุมที่แน่นอน
พบว่าความเร็วของโมเลกุลเงินเกินความเร็วของเสียงและเป็น 500 เมตร/วินาที ข้อเท็จจริงค่อนข้างน่าสนใจ เนื่องจากเป็นเรื่องยากสำหรับคนที่จะรู้สึกถึงความเร็วของการเคลื่อนที่ของอนุภาคในสาร
แก๊สในอุดมคติ
วิจัยต่อดูเหมือนว่าเป็นไปได้เฉพาะในระบบที่สามารถกำหนดพารามิเตอร์ได้โดยการวัดโดยตรงโดยใช้เครื่องมือทางกายภาพ วัดความเร็วด้วยมาตรวัดความเร็ว แต่แนวคิดในการติดมาตรวัดความเร็วกับอนุภาคเดียวนั้นไร้สาระ สามารถวัดได้เฉพาะพารามิเตอร์มหภาคที่เกี่ยวข้องกับการเคลื่อนที่ของอนุภาคเท่านั้น
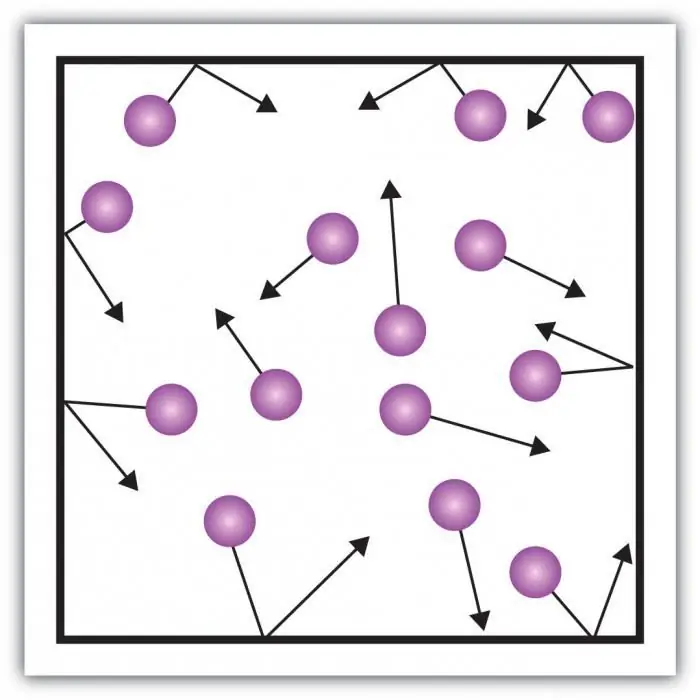
พิจารณาแรงดันแก๊ส แรงกดบนผนังของภาชนะเกิดจากผลกระทบของโมเลกุลของก๊าซในถัง ลักษณะเฉพาะของสถานะก๊าซของสสารอยู่ในระยะห่างขนาดใหญ่เพียงพอระหว่างอนุภาคและปฏิสัมพันธ์ขนาดเล็กของพวกมันระหว่างกัน ช่วยให้คุณวัดแรงดันได้โดยตรง
ระบบใดๆ ของร่างกายที่มีปฏิสัมพันธ์นั้นมีลักษณะเป็นพลังงานศักย์และพลังงานจลน์ของการเคลื่อนไหว ก๊าซจริงเป็นระบบที่ซับซ้อน ความแปรปรวนของพลังงานศักย์ไม่ได้ให้ความสำคัญกับการจัดระบบ ปัญหาสามารถแก้ไขได้ด้วยการแนะนำแบบจำลองที่มีคุณสมบัติเฉพาะของก๊าซ ขจัดความซับซ้อนของการโต้ตอบ
ก๊าซในอุดมคติคือสถานะของสสารที่ปฏิกิริยาของอนุภาคมีน้อยมาก พลังงานศักย์ของการโต้ตอบมีแนวโน้มที่จะเป็นศูนย์ เฉพาะพลังงานของการเคลื่อนไหวซึ่งขึ้นอยู่กับความเร็วของอนุภาคเท่านั้นที่สามารถถือได้ว่ามีนัยสำคัญ
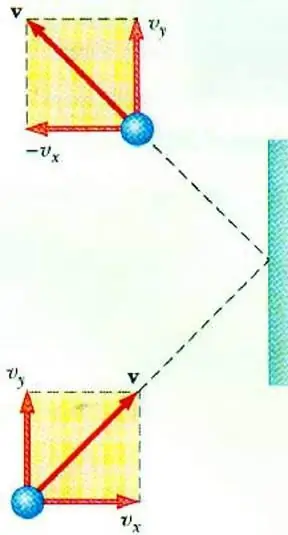
แรงดันแก๊สในอุดมคติ
เพื่อเปิดเผยความสัมพันธ์ระหว่างแรงดันแก๊สกับความเร็วของอนุภาค ทำให้เกิดสมการพื้นฐานของ MKT ของก๊าซในอุดมคติ อนุภาคที่เคลื่อนที่ในเรือเมื่อกระทบกับผนังจะถ่ายโอนแรงกระตุ้นไปยังมันซึ่งค่าที่สามารถกำหนดได้ตามกฎข้อที่สองนิวตัน:
F∆t=2m0vx
การเปลี่ยนแปลงของโมเมนตัมของอนุภาคในระหว่างการกระแทกแบบยืดหยุ่นนั้นสัมพันธ์กับการเปลี่ยนแปลงในองค์ประกอบแนวนอนของความเร็ว F คือแรงที่กระทำจากด้านข้างของอนุภาคบนผนังในช่วงเวลาสั้นๆ t; m0 - มวลอนุภาค
อนุภาคก๊าซทั้งหมดชนกับพื้นผิวของพื้นที่ S ในช่วงเวลา ∆t เคลื่อนที่ไปในทิศทางของพื้นผิวด้วยความเร็ว vx และอยู่ในทรงกระบอกปริมาตร Sυ x Δt. ที่ความเข้มข้นของอนุภาค n โมเลกุลครึ่งหนึ่งเคลื่อนที่ไปทางผนังพอดี อีกครึ่งหนึ่งเคลื่อนที่ไปในทิศทางตรงกันข้าม
เมื่อพิจารณาการชนกันของอนุภาคทั้งหมดแล้ว เราก็สามารถเขียนกฎของนิวตันสำหรับแรงที่กระทำต่อพื้นที่นั้นได้:
F∆t=nm0vx2S∆t
เนื่องจากแรงดันแก๊สถูกกำหนดให้เป็นอัตราส่วนของแรงที่ทำฉากตั้งฉากกับพื้นผิวกับพื้นที่หลัง เราสามารถเขียนได้ว่า:
p=F: S=nm0vx2
ความสัมพันธ์ผลลัพธ์ที่เป็นสมการพื้นฐานของ MKT ไม่สามารถอธิบายทั้งระบบได้ เนื่องจากจะพิจารณาทิศทางการเคลื่อนที่เพียงทิศทางเดียว
จำหน่ายแม็กซ์เวลล์
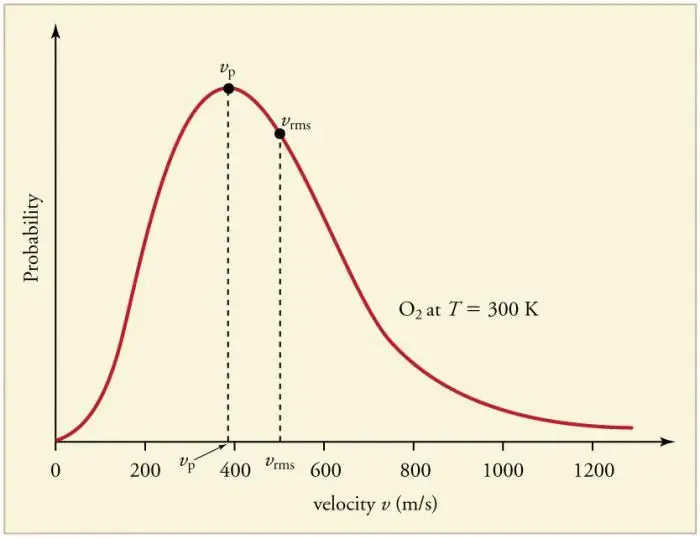
การชนกันของอนุภาคก๊าซกับผนังบ่อยครั้งอย่างต่อเนื่องและทำให้เกิดการกระจายทางสถิติของอนุภาคในแง่ของความเร็ว (พลังงาน) ทิศทางของเวกเตอร์ความเร็วทั้งหมดกลับกลายเป็นว่ามีความน่าจะเป็นเท่ากัน การกระจายนี้เรียกว่าการแจกแจงแบบแมกซ์เวลล์ ในปี พ.ศ. 2403 รูปแบบนี้คือมาจาก J. Maxwell บนพื้นฐานของ MKT พารามิเตอร์หลักของกฎการแจกแจงเรียกว่าความเร็ว: น่าจะเป็น สอดคล้องกับค่าสูงสุดของเส้นโค้ง และค่าเฉลี่ยรูต-ค่าเฉลี่ย-สแควร์ vkv=√‹v2 › - กำลังสองเฉลี่ยของความเร็วอนุภาค
อุณหภูมิก๊าซที่เพิ่มขึ้นสอดคล้องกับความเร็วที่เพิ่มขึ้น
จากข้อเท็จจริงที่ว่าความเร็วทั้งหมดเท่ากัน และโมดูลของมันมีค่าเท่ากัน เราสามารถสมมติได้ว่า:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, จาก: ‹ vx2›=‹v2›: 3
สมการพื้นฐานของ MKT โดยคำนึงถึงค่าเฉลี่ยของแรงดันแก๊สคือ:
p=nm0‹v2›: 3.
ความสัมพันธ์นี้มีความพิเศษตรงที่เป็นตัวกำหนดความสัมพันธ์ระหว่างพารามิเตอร์ด้วยกล้องจุลทรรศน์: ความเร็ว มวลอนุภาค ความเข้มข้นของอนุภาค และความดันก๊าซโดยทั่วไป
โดยใช้แนวคิดเรื่องพลังงานจลน์ของอนุภาค สมการพื้นฐานของ MKT สามารถเขียนใหม่ได้แตกต่างกัน:
p=2nm0‹v2›: 6=2n‹Ek›: 3
ความดันของก๊าซเป็นสัดส่วนกับค่าเฉลี่ยของพลังงานจลน์ของอนุภาค
อุณหภูมิ
น่าสนใจ สำหรับปริมาณก๊าซคงที่ในภาชนะปิด เราสามารถสัมพันธ์กับแรงดันแก๊สและค่าเฉลี่ยของพลังงานการเคลื่อนที่ของอนุภาคได้ ในกรณีนี้ ความดันสามารถวัดได้โดยการวัดพลังงานอนุภาค
ทำอย่างไร? ค่าใดเทียบได้กับพลังงานจลน์ อุณหภูมิกลับกลายเป็นค่าเช่นนี้

อุณหภูมิเป็นตัววัดสถานะความร้อนของสาร ในการวัดนั้นจะใช้เทอร์โมมิเตอร์ซึ่งเป็นพื้นฐานของการขยายตัวทางความร้อนของของเหลวทำงาน (แอลกอฮอล์, ปรอท) เมื่อถูกความร้อน มาตราส่วนเทอร์โมมิเตอร์ถูกสร้างขึ้นจากการทดลอง โดยปกติ เครื่องหมายจะถูกวางไว้บนตำแหน่งที่สอดคล้องกับตำแหน่งของของไหลทำงานในระหว่างกระบวนการทางกายภาพบางอย่างที่เกิดขึ้นที่สภาวะความร้อนคงที่ (น้ำเดือด น้ำแข็งละลาย) เทอร์โมมิเตอร์ต่างกันมีสเกลต่างกัน ตัวอย่างเช่น เซลเซียส ฟาเรนไฮต์

สเกลอุณหภูมิสากล
เทอร์โมมิเตอร์แก๊สถือว่าน่าสนใจกว่าในแง่ของความเป็นอิสระจากคุณสมบัติของสารทำงาน ขนาดของมันไม่ได้ขึ้นอยู่กับชนิดของก๊าซที่ใช้ ในอุปกรณ์ดังกล่าว เราสามารถระบุอุณหภูมิที่ความดันก๊าซมีแนวโน้มเป็นศูนย์ได้โดยสมมุติฐาน การคำนวณแสดงว่าค่านี้สอดคล้องกับ -273.15 oC มาตราส่วนอุณหภูมิ (มาตราส่วนอุณหภูมิสัมบูรณ์หรือระดับเคลวิน) ถูกนำมาใช้ในปี พ.ศ. 2391 อุณหภูมิที่เป็นไปได้ของแรงดันแก๊สเป็นศูนย์ถือเป็นจุดหลักของมาตราส่วนนี้ ส่วนหน่วยของมาตราส่วนเท่ากับค่าหน่วยของมาตราส่วนเซลเซียส การเขียนสมการ MKT พื้นฐานโดยใช้อุณหภูมิจะสะดวกกว่าเมื่อศึกษากระบวนการแก๊ส
ความสัมพันธ์ระหว่างความดันกับอุณหภูมิ
ลองสังเกตดูนะครับสัดส่วนของแรงดันแก๊สกับอุณหภูมิ ในขณะเดียวกันก็พบว่าความดันเป็นสัดส่วนโดยตรงกับความเข้มข้นของอนุภาค:
P=nkT,
โดยที่ T คืออุณหภูมิสัมบูรณ์ k เป็นค่าคงที่เท่ากับ 1.38•10-23J/K.
ค่าพื้นฐานซึ่งมีค่าคงที่สำหรับก๊าซทั้งหมดเรียกว่าค่าคงที่ Boltzmann
เมื่อเปรียบเทียบความกดดันต่ออุณหภูมิและสมการพื้นฐานของก๊าซ MKT เราสามารถเขียนได้ดังนี้
‹Ek›=3kT: 2
ค่าเฉลี่ยของพลังงานจลน์ของการเคลื่อนที่ของโมเลกุลก๊าซเป็นสัดส่วนกับอุณหภูมิของมัน กล่าวคือ อุณหภูมิสามารถเป็นตัววัดพลังงานจลน์ของการเคลื่อนที่ของอนุภาคได้

