กฎ Titius-Bode (บางครั้งเรียกว่ากฎของ Bode) เป็นสมมติฐานที่ว่าวัตถุในระบบการโคจรบางระบบ รวมทั้งดวงอาทิตย์ จะหมุนไปตามกึ่งแกนขึ้นอยู่กับลำดับของดาวเคราะห์ สูตรแนะนำว่า เมื่อขยายออกไปด้านนอก ดาวเคราะห์แต่ละดวงจะอยู่ห่างจากดวงอาทิตย์เป็นสองเท่าเมื่อเทียบกับดวงก่อนหน้า
สมมติฐานทำนายวงโคจรของเซเรส (แถบดาวเคราะห์น้อย) และดาวยูเรนัสได้ถูกต้อง แต่ไม่สามารถระบุวงโคจรของดาวเนปจูนได้ และในที่สุดก็ถูกแทนที่ด้วยทฤษฎีการก่อตัวของระบบสุริยะ ตั้งชื่อตาม Johann Daniel Titius และ Johann Elert Bode

ต้นกำเนิด
การกล่าวถึงครั้งแรกของซีรีส์ที่เกี่ยวกับกฎของโบดสามารถพบได้ใน Elements of Astronomy ของ David Gregory ซึ่งตีพิมพ์ในปี 1715 ในนั้นเขากล่าวว่า: "… สมมติว่าระยะทางจากดวงอาทิตย์สู่โลกแบ่งออกเป็นสิบส่วนเท่า ๆ กันซึ่งระยะห่างของดาวพุธจะอยู่ที่ประมาณสี่จากดาวศุกร์เจ็ดจากดาวอังคารสิบห้าจากดาวพฤหัสบดีห้าสิบสอง และจากดาวเสาร์เก้าสิบห้า" คำแนะนำที่คล้ายกันซึ่งอาจได้รับแรงบันดาลใจจาก Gregory ปรากฏในผลงานที่ตีพิมพ์โดย Christian Wolff ในปี 1724
ในปี ค.ศ. 1764 Charles Bonnet ในหนังสือ Contemplation of Nature กล่าวว่า "เรารู้จักดาวเคราะห์ 17 ดวงที่ประกอบเป็นระบบสุริยะของเรา [นั่นคือดาวเคราะห์หลักและดาวเทียมของพวกมัน] แต่เราไม่แน่ใจว่า พวกเขาไม่มีแล้ว " ในการแปลงานของ Bonnet ในปี ค.ศ. 1766 Johann Daniel Titius ได้เพิ่มย่อหน้าของเขาเองสองย่อหน้าที่ด้านล่างสุดของหน้า 7 และที่ด้านบนของหน้า 8 ไม่พบย่อหน้าที่มีการสอดแทรกใหม่ในข้อความต้นฉบับของ Bonnet: ไม่มีในภาษาอิตาลี หรืองานแปลภาษาอังกฤษ
การค้นพบทิเชียส
ข้อความที่แทรกของ Titius มีสองส่วน ขั้นแรกอธิบายลำดับระยะห่างของดาวเคราะห์จากดวงอาทิตย์ นอกจากนี้ยังมีคำสองสามคำเกี่ยวกับระยะทางจากดวงอาทิตย์ถึงดาวพฤหัสบดี แต่นี่ไม่ใช่จุดสิ้นสุดของข้อความ
ควรพูดสักสองสามคำเกี่ยวกับสูตรของกฎ Titius-Bode ให้ความสนใจกับระยะห่างระหว่างดาวเคราะห์และพบว่าเกือบทั้งหมดแยกออกจากกันในสัดส่วนที่สอดคล้องกับขนาดร่างกายของดาวเคราะห์ แบ่งระยะทางจากดวงอาทิตย์ถึงดาวเสาร์ด้วย 100 ส่วน; จากนั้นดาวพุธจะถูกแยกออกจากดวงอาทิตย์สี่ส่วน ดาวศุกร์ - เป็น 4 + 3=7 ส่วนดังกล่าว โลก - โดย 4+6=10; ดาวอังคาร - โดย 4+12=16.
แต่โปรดทราบว่าจากดาวอังคารถึงดาวพฤหัสบดีมีความคลาดเคลื่อนจากความก้าวหน้าที่แม่นยำเช่นนี้ อวกาศ 4+24=28 ส่วนดังกล่าวตามมาจากดาวอังคาร แต่จนถึงขณะนี้ยังไม่มีการค้นพบดาวเคราะห์ดวงเดียวที่นั่น แต่ลอร์ดสถาปนิกควรปล่อยให้สถานที่นี้ว่างเปล่าหรือไม่? ไม่เคย. ดังนั้นสมมติว่าพื้นที่นี้เป็นของดวงจันทร์ดาวอังคารที่ยังไม่ถูกค้นพบโดยไม่ต้องสงสัย และเสริมว่าบางทีดาวพฤหัสบดียังคงมีดวงจันทร์ดวงเล็กๆ อยู่รอบๆ ซึ่งกล้องยังไม่ได้เห็น

ลางสังหรณ์
ในปี ค.ศ. 1772 โยฮันน์ เอเลิร์ต โบเด (Johann Elert Bode) เมื่ออายุได้ 25 ปี ได้จัดทำบทสรุปทางดาราศาสตร์ฉบับที่สอง Anleitung zur Kenntniss des gestirnten Himmels ("คู่มือสู่ความรู้เกี่ยวกับท้องฟ้าเต็มไปด้วยดวงดาว") ซึ่งเขา เพิ่มเชิงอรรถต่อไปนี้ซึ่งเดิมไม่มีแหล่งที่มา แต่ระบุไว้ในเวอร์ชันที่ใหม่กว่า ในบันทึกความทรงจำของ Bode เราสามารถหาการอ้างอิงถึง Titius ด้วยการรับรู้อย่างชัดเจนถึงอำนาจของเขา

ลางสังหรณ์ความคิดเห็น
นี่คือวิธีที่กฎของ Titius-Bode ในการนำเสนอของเสียงหลัง: หากระยะทางจากดวงอาทิตย์ถึงดาวเสาร์เท่ากับ 100 ดาวพุธจะถูกแยกออกจากดวงอาทิตย์ด้วยสี่ส่วนดังกล่าว ดาวศุกร์ - 4+3=7. โลก - 4+6=10. ดาวอังคาร - 4+12=16.
ตอนนี้มีช่องว่างในการดำเนินการตามลำดับนี้ หลังจากดาวอังคารมีช่องว่างตามหลังด้วยการคำนวณ 4+24=28 ซึ่งยังไม่มีใครเห็นดาวเคราะห์ดวงเดียว เราเชื่อได้ไหมว่าผู้ก่อตั้งจักรวาลปล่อยให้พื้นที่นี้ว่าง? แน่นอนไม่ จากนี้ไปเรามาถึงระยะทางของดาวพฤหัสบดีในรูปแบบการคำนวณ 4+48=52 และในที่สุดก็ถึงระยะทางของดาวเสาร์ - 4+96=100.

ข้อความสองคำนี้เกี่ยวกับประเภทเฉพาะและรัศมีการโคจรดูเหมือนมาจากโบราณดาราศาสตร์. หลายทฤษฎีเหล่านี้มีมาตั้งแต่ก่อนศตวรรษที่สิบเจ็ด
อิทธิพล
Titius เป็นนักเรียนของ Christian Freiherr von Wolff นักปรัชญาชาวเยอรมัน (1679-1754) ส่วนที่สองของข้อความที่แทรกในงานของ Bonnet อ้างอิงจากผลงานของ von Wolff ในปี 1723 Vernünftige Gedanken von den Wirkungen der Natur
วรรณกรรมของศตวรรษที่ 20 มอบหมายการประพันธ์กฎ Titius-Bode ให้กับนักปรัชญาชาวเยอรมัน ถ้าเป็นเช่นนั้น ทิเชียสสามารถเรียนรู้จากเขาได้ เอกสารอ้างอิงที่เก่ากว่าอีกฉบับหนึ่งเขียนโดย James Gregory ในปี 1702 ในหนังสือ Astronomiae Physicae et geometryae Elementa ซึ่งลำดับของระยะห่างของดาวเคราะห์ 4, 7, 10, 16, 52 และ 100 กลายเป็นความก้าวหน้าทางเรขาคณิตของอัตราส่วน 2
นี่คือสูตรที่ใกล้เคียงที่สุดของนิวตัน และยังพบในงานเขียนของ Benjamin Martin และ Thomas Ceard หลายปีก่อนที่หนังสือของ Bonnet จะตีพิมพ์ในเยอรมนี
งานต่อไปและความหมายเชิงปฏิบัติ
Titius และ Bode หวังว่ากฎหมายจะนำไปสู่การค้นพบดาวเคราะห์ดวงใหม่ และแท้จริงแล้ว การค้นพบดาวยูเรนัสและเซเรสซึ่งระยะห่างระหว่างกันซึ่งตกลงกันเป็นอย่างดีกับกฎหมาย ส่งผลให้โลกวิทยาศาสตร์ยอมรับ
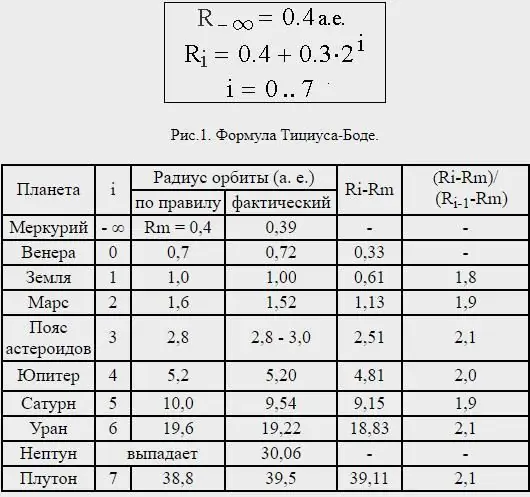
อย่างไรก็ตาม ระยะทางของดาวเนปจูนนั้นไม่สอดคล้องกันอย่างมาก และที่จริงแล้วดาวพลูโตซึ่งตอนนี้ไม่ถือว่าเป็นดาวเคราะห์นั้นอยู่ในระยะทางเฉลี่ยที่ใกล้เคียงกับกฎ Titius-Bode ที่คาดการณ์ไว้สำหรับดาวเคราะห์ดวงถัดไปนอกดาวยูเรนัส
กฎที่ตีพิมพ์ครั้งแรกนั้นค่อนข้างพอใจโดยดาวเคราะห์ที่รู้จักทั้งหมด - ดาวพุธและดาวเสาร์ - โดยมีช่องว่างระหว่างดาวเคราะห์ดวงที่สี่และห้า ซึ่งถือได้ว่าเป็นตัวเลขที่น่าสนใจแต่ไม่ได้มีความสำคัญอย่างยิ่งจนกระทั่งมีการค้นพบดาวยูเรนัสในปี พ.ศ. 2324 ซึ่งเข้ากับซีรีส์
จากการค้นพบนี้ Bode ได้เรียกร้องให้มีการค้นหาดาวเคราะห์ดวงที่ห้า Ceres ซึ่งเป็นวัตถุที่ใหญ่ที่สุดในแถบดาวเคราะห์น้อยถูกพบในตำแหน่งที่คาดการณ์ของ Bode ในปี 1801 กฎของลางบอกเหตุได้รับการยอมรับอย่างกว้างขวางจนกระทั่งมีการค้นพบดาวเนปจูนในปี พ.ศ. 2389 และพบว่าไม่สอดคล้องกับกฎหมาย
ในขณะเดียวกัน ดาวเคราะห์น้อยจำนวนมากที่ค้นพบในแถบแถบนั้นก็ได้พาดผ่านเซเรสออกจากรายชื่อดาวเคราะห์ กฎของลางบอกเหตุโดยนักดาราศาสตร์และนักตรรกวิทยา Charles Sanders Peirce ในปี 1898 เป็นตัวอย่างของการให้เหตุผลที่ผิดพลาด

การพัฒนาของปัญหา
การค้นพบดาวพลูโตในปี 1930 ทำให้ปัญหาซับซ้อนยิ่งขึ้น แม้ว่ามันจะไม่ตรงกับตำแหน่งที่กฎของโบดทำนายไว้ แต่ก็เกี่ยวกับตำแหน่งที่กฎหมายทำนายไว้สำหรับดาวเนปจูน อย่างไรก็ตาม การค้นพบแถบไคเปอร์ในเวลาต่อมา และโดยเฉพาะอย่างยิ่งวัตถุ Eris ซึ่งมีมวลมากกว่าดาวพลูโตแต่ไม่เป็นไปตามกฎของโบด กลับทำให้สูตรนี้เสียชื่อเสียง
ผลงานของ Serda
นิกายเยซูอิต โธมัส เซอร์ดาเปิดสอนหลักสูตรดาราศาสตร์ที่มีชื่อเสียงในบาร์เซโลนาในปี 1760 ที่เก้าอี้พระราชาแห่งคณิตศาสตร์ที่วิทยาลัย Sant Jaume de Cordelle (วิทยาลัยจักรวรรดิและราชวงศ์แห่งขุนนางแห่งคอร์เดลล์) ใน Tratado ของ Cerdas ระยะทางของดาวเคราะห์ปรากฏขึ้น ซึ่งได้มาจากการใช้กฎข้อที่สามของ Kepler ด้วยความแม่นยำ 10-3
ถ้าเราใช้ระยะทางจากโลกถึง 10 และปัดเศษขึ้นเป็นจำนวนเต็ม ความก้าวหน้าทางเรขาคณิต [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2 จาก n=2 ถึง n=8 อาจแสดงได้ และการใช้การเคลื่อนที่ที่สมมติขึ้นเป็นวงกลมกับความผิดปกติของเคปเลอร์ ค่า Rn ที่สัมพันธ์กับอัตราส่วนของดาวเคราะห์แต่ละดวงสามารถรับได้เป็น rn=(Rn - R1) / (Rn-1 - R1) ส่งผลให้ 1.82; 1, 84; 1, 86; 1.88 และ 1.90 โดยที่ rn=2 - 0.02 (12 - n) เป็นความสัมพันธ์ที่ชัดเจนระหว่างความต่อเนื่องของ Keplerian และกฎ Titius-Bode ซึ่งถือเป็นความบังเอิญทางตัวเลขแบบสุ่ม ผลการคำนวนใกล้เป็น 2 แต้ม แต่ดิวซ์อาจจะนับว่าเป็นการปัดเศษของเลข 1, 82.

ความเร็วเฉลี่ยของดาวเคราะห์จาก n=1 ถึง n=8 จะลดระยะห่างจากดวงอาทิตย์และแตกต่างจากการลดลงสม่ำเสมอที่ n=2 เพื่อฟื้นตัวจาก n=7 (การสั่นพ้องของวงโคจร) ส่งผลต่อระยะทางจากดวงอาทิตย์ถึงดาวพฤหัสบดี อย่างไรก็ตาม ระยะห่างระหว่างวัตถุอื่น ๆ ทั้งหมดภายในกรอบของกฎที่มีชื่อเสียงซึ่งบทความทุ่มเทนั้นถูกกำหนดโดยพลวัตทางคณิตศาสตร์นี้เช่นกัน
เชิงทฤษฎี
ไม่มีคำอธิบายเชิงทฤษฎีที่แน่ชัดซึ่งอยู่ภายใต้กฎ Titius-Bode แต่เป็นไปได้ว่าด้วยการรวมกันของการสั่นพ้องของวงโคจรและระดับความเป็นอิสระ ระบบดาวเคราะห์ใดๆ ที่เสถียรมีโอกาสสูงที่จะทำซ้ำแบบจำลองที่อธิบายไว้ใน ทฤษฎีนี้โดยนักวิทยาศาสตร์ทั้งสอง
เพราะนี่อาจเป็นเรื่องบังเอิญทางคณิตศาสตร์และไม่ใช่ "กฎแห่งธรรมชาติ" บางครั้งจึงเรียกว่ากฎมากกว่า "กฎ" อย่างไรก็ตาม Alan Boss นักดาราศาสตร์ฟิสิกส์ให้เหตุผลว่านี่เป็นเพียงบังเอิญ และวารสารวิทยาศาสตร์ดาวเคราะห์ Icarus ไม่ยอมรับบทความที่พยายามจัดหา "กฎหมาย" เวอร์ชันปรับปรุงอีกต่อไป
การสั่นพ้องของวง
การสั่นพ้องของวงโคจรจากวัตถุที่โคจรรอบใหญ่ทำให้เกิดพื้นที่รอบดวงอาทิตย์ที่ไม่มีวงโคจรที่มั่นคงในระยะยาว ผลการจำลองการก่อตัวของดาวเคราะห์สนับสนุนแนวคิดที่ว่าระบบดาวเคราะห์ที่มีความเสถียรซึ่งสุ่มเลือกมานั้นน่าจะเป็นไปตามกฎของทิเชียส-โบเด

ดูบรูลและกราเนอร์
Dubrulle และ Graner แสดงให้เห็นว่ากฎระยะห่างของกฎกำลังสามารถเป็นผลมาจากแบบจำลองเมฆที่ยุบตัวของระบบดาวเคราะห์ที่มีความสมมาตรสองแบบ: ค่าคงที่การหมุน (เมฆและเนื้อหามีความสมมาตรตามแกน) และความแปรปรวนของมาตราส่วน (เมฆและ เนื้อหาจะเหมือนกันทุกขนาด).
หลังนี้เป็นคุณลักษณะของปรากฏการณ์มากมายที่คิดว่าจะมีบทบาทในการก่อตัวดาวเคราะห์ เช่น ความปั่นป่วน ระยะทางจากดวงอาทิตย์ไปยังดาวเคราะห์ของระบบสุริยะที่เสนอโดย Titius และ Bode ไม่ได้แก้ไขในกรอบของการศึกษา Dubrulle และ Graner

