ฟังก์ชันเชิงเส้นคือเส้นตรงที่ลากไปตามพื้นผิว สามารถแบ่งออกเป็นประเภทต่างๆและรุ่น ด้านล่างเราจะพิจารณาสูตรในการได้มาซึ่งรวมถึงการบรรลุความสมบูรณ์แบบในระนาบ ในภาพวาด คุณสามารถยืนยันสิ่งนี้ได้อย่างเต็มที่และเข้าใจว่าควรมีลักษณะอย่างไร
ฟังก์ชันเชิงเส้น y=kx + b
ค่านี้เป็นการวัดตัวแปรที่แม่นยำในมุมมองเดียว การเพิ่มขึ้นหมายถึงคุณสมบัติพื้นฐานของฟังก์ชันเชิงเส้น ซึ่งจะกลายเป็นสัดส่วนกับอาร์กิวเมนต์ที่เพิ่มขึ้น กล่าวอีกนัยหนึ่ง ฟังก์ชันแสดงถึงลักษณะทั่วไปของสัดส่วนโดยตรง เส้นตรงคือกราฟของฟังก์ชันเชิงเส้น นี่คือที่มาของชื่อ ตัวแปรจริงตัวหนึ่งสัมผัสกับฟังก์ชันจริงอีกตัว
คุณสมบัติ
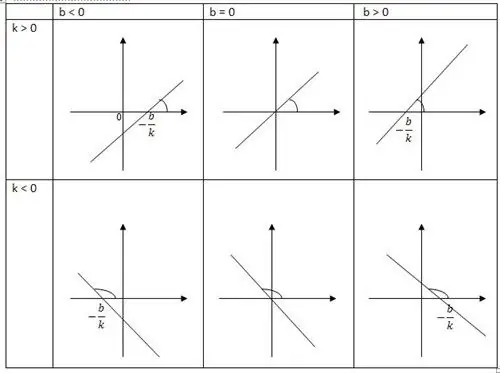
ฟังก์ชันลิเนียร์คือตัวสร้างของเส้นตรงซึ่งมีทิศทางเป็นบวกของแกน x หนึ่งในปัจจัยความชันที่กำหนดคือ k ซึ่งกำหนดแทนเจนต์ของมุม a เส้นตรงที่เกิดขึ้นในทิศทางบวกของแกน x คือ k พิกัดอื่น b หมายถึงพิกัดจุดเช่นเดียวกับจุดตัดของเส้นที่มีแกน
ฟังก์ชันไม่เชิงเส้นคืออะไร
ฟังก์ชันที่ไม่เชิงเส้นเรียกว่าไม่เป็นเชิงเส้น นี่คือความสัมพันธ์ทางคณิตศาสตร์ระหว่างตัวแปร สิ่งที่ไม่เชิงเส้นไม่สามารถแสดงเป็น y=ax + b คำนี้ใช้ในช่วงเวลาที่จำเป็นในการศึกษากรณีทั่วไป กระบวนการนี้เริ่มต้นด้วยองศาที่ต่ำกว่า ในกรณีนี้จะพิจารณาการแก้ไขกำลังสอง ฟังก์ชันดังกล่าวมีความโค้งต่อเนื่อง
สมการไม่เชิงเส้นที่พิจารณานั้นเป็นกฎเกณฑ์ ตัวอย่างของฟังก์ชันไม่เชิงเส้นคือ y=x2 มักใช้คำว่า "ฟังก์ชันเชิงเส้น" โดยมีการปรับแต่งและเติมคำว่า "เป็นเนื้อเดียวกัน" สามารถใช้กับการแมปเชิงเส้นที่แน่นอนของ X ซึ่งเป็นสเปซเวกเตอร์ ฟังก์ชันเชิงเส้นคือทั้งระบบที่ชอบ

