ลวดลายหรือลวดลายเรขาคณิตธรรมชาติปรากฏเป็นรูปร่างซ้ำๆ ซึ่งบางครั้งสามารถอธิบายหรือแสดงด้วยแบบจำลองทางคณิตศาสตร์ได้
เรขาคณิตในธรรมชาติและชีวิตมีหลายรูปแบบ เช่น สมมาตร เกลียว หรือคลื่น
ประวัติศาสตร์
นักปรัชญาและนักวิทยาศาสตร์ชาวกรีกโบราณ - Pythagoras, Empedocles และ Plato ได้ตั้งคำถามเกี่ยวกับเรขาคณิตในธรรมชาติเป็นครั้งแรก โดยการวิเคราะห์ตัวอย่างรูปทรงเรขาคณิตที่คาดเดาได้หรือในอุดมคติในพืชและสัตว์ พวกเขาพยายามแสดงให้เห็นถึงความเป็นระเบียบและความสมมาตรในธรรมชาติ
ความพยายามที่จะศึกษาเรขาคณิตในธรรมชาติแบบสมัยใหม่เริ่มต้นขึ้นในศตวรรษที่ 19 ด้วยความพยายามของนักฟิสิกส์ชาวเบลเยียม Joseph Plateau ผู้พัฒนาแนวคิดเรื่องพื้นผิวขั้นต่ำของฟองสบู่ ความพยายามสมัยใหม่ครั้งแรกมุ่งเน้นไปที่การแสดงรูปทรงเรขาคณิตในอุดมคติและคาดเดาได้ จากนั้นจึงหันไปพัฒนาแบบจำลองที่ทำนายลักษณะที่ปรากฏและการปรากฎของเรขาคณิตในธรรมชาติ
ในศตวรรษที่ 20 นักคณิตศาสตร์ Alan Turing ได้ศึกษาเกี่ยวกับกลไกของการสร้างรูปร่าง (morphogenesis) ซึ่งอธิบายลักษณะที่ปรากฏของสัตว์ลวดลายต่างๆ ลายเส้น จุด อีกไม่นานนักชีววิทยา Aristide Lindenmeier ร่วมกับนักคณิตศาสตร์ Benoit Mandelbrot จะทำงานเกี่ยวกับเศษส่วนทางคณิตศาสตร์ที่ทำซ้ำรูปแบบการเติบโตของพืชบางชนิดรวมถึงต้นไม้
วิทยาศาสตร์
วิทยาศาสตร์สมัยใหม่ (คณิตศาสตร์ ฟิสิกส์ และเคมี) ด้วยความช่วยเหลือของเทคโนโลยีและแบบจำลอง ไม่เพียงแต่พยายามจะอธิบาย แต่ยังรวมถึงการทำนายรูปแบบเรขาคณิตที่พบในธรรมชาติด้วย
รูปร่างและสีของสิ่งมีชีวิตมากมาย เช่น นกยูง นกฮัมมิ่งเบิร์ด และเปลือกหอย ไม่เพียงแต่สวยงามเท่านั้น แต่ยังถูกต้องทางเรขาคณิต ซึ่งดึงดูดความอยากรู้ของนักวิทยาศาสตร์ ความงามที่เราสังเกตได้ในธรรมชาติสามารถเกิดขึ้นได้ตามธรรมชาติทางคณิตศาสตร์
รูปแบบธรรมชาติที่สังเกตพบในวิชาคณิตศาสตร์อธิบายโดยทฤษฎีความโกลาหล ซึ่งทำงานกับเกลียวและเศษส่วน รูปแบบดังกล่าวเป็นไปตามกฎของฟิสิกส์ นอกจากนี้ ฟิสิกส์และเคมี ใช้คณิตศาสตร์เชิงนามธรรมทำนายรูปร่างของคริสตัล ทั้งจากธรรมชาติและประดิษฐ์
ชีววิทยาอธิบายเรขาคณิตในธรรมชาติโดยการคัดเลือกโดยธรรมชาติ โดยลักษณะปกติ เช่น ลายทาง จุด สีสดใส สามารถอธิบายได้ด้วยความจำเป็นในการปิดบังหรือส่งสัญญาณ
ประเภทของลวดลาย
โดยธรรมชาติแล้ว มีลวดลายซ้ำๆ มากมายที่ปรากฏในรูปทรงเรขาคณิตต่างๆ ประเภทของความสม่ำเสมอพื้นฐานของเรขาคณิตในธรรมชาติ รูปภาพ และคำอธิบายอยู่ด้านล่าง
สมมาตร. รูปทรงเรขาคณิตนี้มีลักษณะทั่วไปมากที่สุดแห่งหนึ่ง พบมากในสัตว์กระจกสมมาตร - ผีเสื้อ, ด้วง, เสือ, นกฮูก นอกจากนี้ยังพบในพืชเช่นใบเมเปิ้ลหรือดอกกล้วยไม้ นอกจากนี้ เรขาคณิตสมมาตรในธรรมชาติอาจเป็นแนวรัศมี 5 แฉก หรือ 6 เท่า เช่น เกล็ดหิมะ

เศษส่วน. ในวิชาคณิตศาสตร์ สิ่งเหล่านี้เป็นสิ่งก่อสร้างที่คล้ายคลึงกันซึ่งไม่มีที่สิ้นสุด โดยธรรมชาติแล้ว เป็นไปไม่ได้ที่จะตรวจจับรูปแบบที่เกิดซ้ำตัวเองไม่รู้จบ ดังนั้นการประมาณรูปแบบเศษส่วนจึงเรียกว่าเศษส่วนทางเรขาคณิตในธรรมชาติ เรขาคณิตดังกล่าวสามารถสังเกตได้ในธรรมชาติในใบเฟิร์น บร็อคโคลี่ ผลไม้สับปะรด
เกลียว. รูปแบบเหล่านี้พบได้บ่อยโดยเฉพาะในหมู่หอยและหอยทาก นักวิทยาศาสตร์สังเกตรูปร่างก้นหอยในอวกาศ เช่น ดาราจักรก้นหอย เกลียวนี้เรียกว่าอัตราส่วนทองคำของฟีโบนักชี

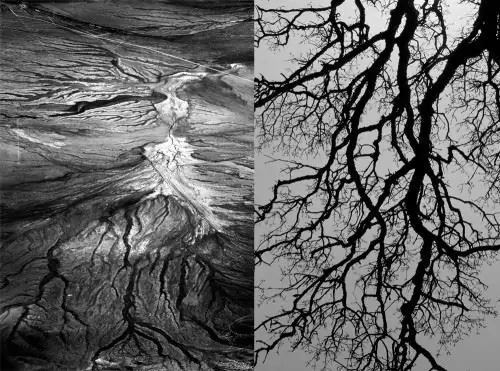
คดเคี้ยว. ความสุ่มของระบบไดนามิกในวิชาคณิตศาสตร์แสดงออกในรูปแบบต่างๆ เช่น ทางคดเคี้ยวและการไหล เรขาคณิตธรรมชาติจะอยู่ในรูปของเส้นโค้งหักหรือค่อนข้างโค้ง เช่น กระแสน้ำ
คลื่น. เกิดจากการรบกวนและการเคลื่อนที่ของอากาศ กระแสลม แผ่กระจายไปทั้งทางอากาศและทางน้ำ โดยธรรมชาติแล้ว สิ่งเหล่านี้ไม่ได้เป็นเพียงคลื่นทะเลเท่านั้น แต่ยังรวมถึงเนินทรายในทะเลทรายด้วย ซึ่งสามารถสร้างรูปทรงเรขาคณิตได้ เช่น เส้น เสี้ยว และพาราโบลา
โมเสก. สร้างขึ้นโดยการทำซ้ำองค์ประกอบเดียวกันบนพื้นผิว เรขาคณิตของโมเสคในสัตว์ป่าพบได้ในผึ้ง: พวกมันสร้างรังของรวงผึ้ง - เซลล์ซ้ำ

การก่อตัวของลวดลาย
ในทางชีววิทยา การก่อตัวของสีเรขาคณิตนั้นเกิดจากกระบวนการคัดเลือกโดยธรรมชาติ ย้อนกลับไปในช่วงกลางศตวรรษที่ 20 อลัน ทัวริง สามารถอธิบายกลไกสำหรับการปรากฏตัวของจุดและลายทางในสีของสัตว์ - เขาเรียกมันว่าแบบจำลองการกระจายปฏิกิริยา เซลล์ในร่างกายบางเซลล์มียีนที่ควบคุมโดยปฏิกิริยาเคมี Morphogen นำไปสู่การก่อตัวของพื้นที่ผิวที่มีเม็ดสีเข้ม (จุดและลาย) หากมีมอร์โฟเจนอยู่ในทุกเซลล์ผิว - สีของเสือดำจะได้รับ หากมีไม่สม่ำเสมอ - เสือดาวลายจุดปกติ

